|
Concept of Friction Factor in a pipe flow:
- The friction factor in the case of a pipe flow was already mentioned in lecture 26.
- We will elaborate further on friction factor or friction coefficient in this section.
- Skin friction coefficient for a fully developed flow through a closed duct is defined as
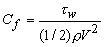 |
(35.1) |
where, V is the average velocity of flow given by  , Q and A are the volume flow rate through the duct and the cross-sectional area of the duct respectively. , Q and A are the volume flow rate through the duct and the cross-sectional area of the duct respectively.
From a force balance of a typical fluid element (Fig. 35.1) in course of its flow through a duct of constant cross-sectional area, we can write
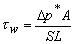 |
(35.2) |
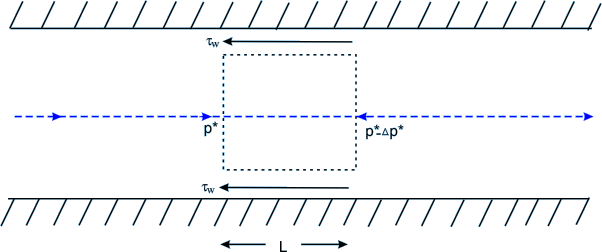
FIG 35.1 Force Balance of a fluid element in the course of flow through a duct
where,
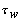 is the shear stress at the wall and is the shear stress at the wall and
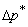 is the piezometric pressure drop over a length of L . A and S are respectively the cross-sectional area and wetted perimeter of the duct. is the piezometric pressure drop over a length of L . A and S are respectively the cross-sectional area and wetted perimeter of the duct.
Substituting the expression (35.2) in Eq. (35.1), we have,
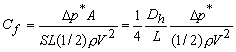 |
(35.3) |
where, 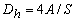 and is known as the hydraulic diameter . and is known as the hydraulic diameter .
In case of a circular pipe, Dh=D, the diameter of the pipe. The coefficient Cf defined by Eqs (35.1) or (35.3) is known as Fanning's friction factor .
- To do away with the factor 1/4 in the Eq. (35.3), Darcy defined a friction factor f (Darcy's friction factor) as
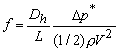 |
(35.4) |
- Comparison of Eqs (35.3) and (35.4) gives
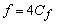 . Equation (35.4) can be written for a pipe flow as . Equation (35.4) can be written for a pipe flow as
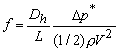 |
(35.5) |
- Equation (35.5) is written in a different fashion for its use in the solution of pipe flow problems in practice as
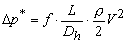 |
(35.6a) |
or in terms of head loss (energy loss per unit weight)
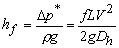 |
(35.6b) |
where, hf represents the loss of head due to friction over the length L of the pipe.
- Equation (35.6b) is frequently used in practice to determine hf
- In order to evaluate hf, we require to know the value of f. The value of f can be determined from Moody's Chart.
|