• In analogy with the coefficient of viscosity for laminar flow, J. Boussinesq introduced a mixing coefficient for the Reynolds stress term, defined as

• Using the shearing stresses can be written as
  

such that the equation

may be written as

The term ν_t is known as eddy viscosity and the model is known as eddy viscosity model .

• Unfortunately the value of ν_t is not known. The term ν is a property of the fluid whereas ν_t is attributed to random fluctuations and is not a property of the fluid. However, it is necessary to find out empirical relations between ν_t, and the mean velocity. The following section discusses relation between the aforesaid apparent or eddy viscosity and the mean velocity components

• Consider a fully developed turbulent boundary layer . The stream wise mean velocity varies only from streamline to streamline. The main flow direction is assumed parallel to the x-axis (Fig. 33.4).
  
• The time average components of velocity are given by . The fluctuating component of transverse velocity transports mass and momentum across a plane at y₁ from the wall. The shear stress due to the fluctuation is given by
  

• Fluid, which comes to the layer y₁ from a layer (y₁- l) has a positive value of . If the lump of fluid retains its original momentum then its velocity at its current location y₁ is smaller than the velocity prevailing there. The difference in velocities is then

Fig. 33.4   One-dimensional parallel flow and Prandtl's mixing length hypothesis

The above expression is obtained by expanding the function 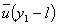in a Taylor series and neglecting all higher order terms and higher order derivatives. l is a small length scale known as Prandtl's mixing length . Prandtl proposed that the transverse displacement of any fluid particle is, on an average, 'l' .