- We define the friction velocity,
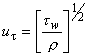 |
(33.11b) |
as our velocity scale. Once  is specified, the structure of the sub layer is specified. It has been confirmed experimentally that the turbulent intensity distributions are scaled with is specified, the structure of the sub layer is specified. It has been confirmed experimentally that the turbulent intensity distributions are scaled with  . For example, maximum value of the
. For example, maximum value of the 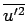 is always about is always about 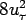 . The relationship between . The relationship between  and the and the 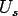 can be determined from Eqs (33.11a) and (33.11b) as can be determined from Eqs (33.11a) and (33.11b) as
Let us assume
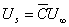 . Now we can write . Now we can write
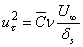 where where 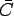 is a proportionality constant is a proportionality constant |
(33.12a) |
or
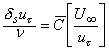 |
(33.12b) |
Hence, a non-dimensional coordinate may be defined as,
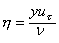 which will help us estimating different zones in a turbulent flow. The thickness of laminar sublayer or viscous sublayer is considered to be which will help us estimating different zones in a turbulent flow. The thickness of laminar sublayer or viscous sublayer is considered to be 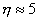 . .
Turbulent effect starts in the zone of 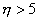 and in a zone of and in a zone of 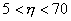 , laminar and turbulent motions coexist. This domain is termed as buffer zone. Turbulent effects far outweight the laminar effect in the zone beyond , laminar and turbulent motions coexist. This domain is termed as buffer zone. Turbulent effects far outweight the laminar effect in the zone beyond 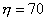 and this regime is termed as turbulent core . and this regime is termed as turbulent core .
|