|
Blasius Flow Over A Flat Plate
- The classical problem considered by H. Blasius was
- Two-dimensional, steady, incompressible flow over a flat plate at zero angle of incidence with respect to the uniform stream of velocity
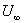 . .
- The fluid extends to infinity in all directions from the plate.
The physical problem is already illustrated in Fig. 28.1
- Blasius wanted to determine
(a) the velocity field solely within the boundary layer,
(b) the boundary layer thickness
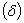 , ,
(c) the shear stress distribution on the plate, and
(d) the drag force on the plate.
- The Prandtl boundary layer equations in the case under consideration are
The boundary conditions are
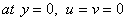 |
(28.16) |
- Note that the substitution of the term
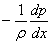 in the original boundary layer momentum equation in terms of the free stream velocity produces in the original boundary layer momentum equation in terms of the free stream velocity produces
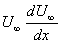 which is equal to zero. which is equal to zero.
- Hence the governing Eq. (28.15) does not contain any pressure-gradient term.
- However, the characteristic parameters of this problem are
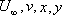 that is, that is,
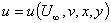
- This relation has five variables
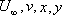 . .
- It involves two dimensions, length and time.
- Thus it can be reduced to a dimensionless relation in terms of (5-2) =3 quantities ( Buckingham Pi Theorem)
- Thus a similarity variables can be used to find the solution
- Such flow fields are called self-similar flow field .
|