|
Low Reynolds Number Flow Around a Sphere
- Stokes obtained the solution for the pressure and velocity field for the slow motion of a viscous fluid past a sphere. In his analysis, Stokes neglected the inertia terms of Navier-Stokes equations.
- Avoiding details, integrating the pressure distribution and the shearing stress over the surface of a sphere of radius R , Stokes found that the drag D of the sphere, which is placed in a parallel stream of uniform velocity
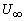 , is given by , is given by
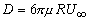 |
(27.1) |
This is the well-known Stokes' equation for the drag of a sphere.
- It can be shown that one third of the total drag is due to pressure distribution and the remaining two third arises from frictional forces. If the drag coefficient is defined according to the relation
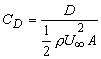 |
(27.2) |
where 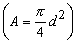 is the frontal area of the sphere, then is the frontal area of the sphere, then
or 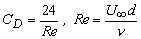 |
(27.3) |
- A comparison between Stokes' drag coefficient in Eq. (27.3) and experiments is shown in Fig. 27.1. The approximate solution due to Stokes' is valid for Re < 1.
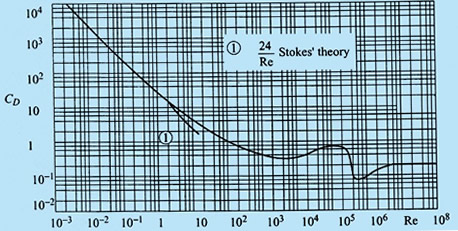 FIG 27.1 - Comparison between Stokes' drag coefficient and experimental drag coefficient
FIG 27.1 - Comparison between Stokes' drag coefficient and experimental drag coefficient
- An important application of Stokes' law is the determination of viscosity of a viscous fluid by measuring the terminal velocity of a falling sphere. In this device, a sphere is dropped in a transparent cylinder containing the fluid under test. If the specific weight of the sphere is close to that of the liquid, the sphere will approach a small constant speed after being released in the fluid. Now we can apply Stokes' law for steady creeping flow around a sphere where the drag force on the sphere is given by Eq. (27.1).
- With the sphere, falling at a constant speed, the acceleration is zero. This signifies that the falling body has attained terminal velocity and we can say that the sum of the buoyant force and drag force is equal to weight of the body.
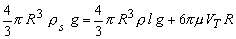 |
(27.4) |
where ρs is the density of the sphere, ρl is density of the liquid and VT is the terminal velocity.
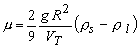 |
(27.5) |
The terminal velocity VT can be measured by observing the time for the sphere to cross a known distance between two points after its acceleration has ceased.
|