Couette Flow

Couette flow is the flow between two parallel plates (Fig. 26.1). Here, one plate is at rest and the other is moving with a velocity U . Let us assume the plates are infinitely large in z direction, so the z dependence is not there.

The governing equation is

flow is independent of any variation in z-direction.
The boundary conditions are ---(i)At y = 0, u = 0 (ii)At y = h, u = U.

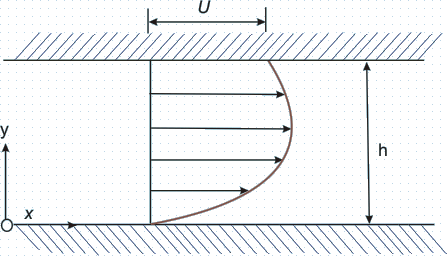
FIG 26.1 Couette flow between two parallel flat plates

• We get,

Invoking the condition (at y = 0, u = 0), 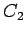becomes equal to zero.

Invoking the other condition (at y = h, u = U),

So,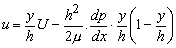

(26.1)

Equation (26.1) can also be expressed in the form

or,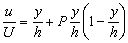

(26.2a)

Where     

,

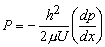Equation (26.2a) describes the velocity distribution in non-dimensional form across the channel with P as a parameter known as the non-dimensional pressure gradient .

• When P = 0, the velocity distribution across the channel is reduced to

This particular case is known as simple Couette flow.

• When P > 0 , i.e. for a negative or favourable pressure gradient in the direction of motion, the velocity is positive over the whole gap between the channel walls. For negative value of P ( P < 0 ), there is a positive or adverse pressure gradient in the direction of motion and the velocity over a portion of channel width can become negative and back flow may occur near the wall which is at rest. Figure 26.2a shows the effect of dragging action of the upper plate exerted on the fluid particles in the channel for different values of pressure gradient.

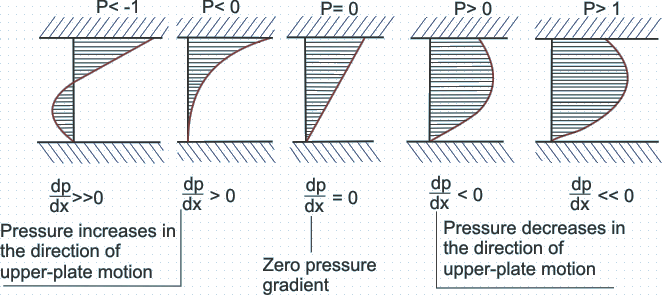
FIG 26.2a - Velocity profile for the Couette flow for various values of pressure gradient