|
Parallel Flow in a Straight Channel
Consider steady flow between two infinitely broad parallel plates as shown in Fig. 25.2.
Flow is independent of any variation in z direction, hence, z dependence is gotten rid of and Eq. (25.11) becomes
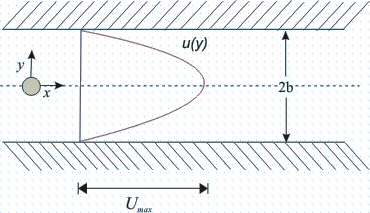
FIG 25.2 Parallel flow in a straight channel
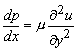 |
(25.12) |
The boundary conditions are at y = b, u = 0; and y = -b, u = O.
- From Eq. (25.12), we can write
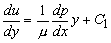 |
|
or 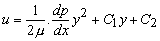 |
|
- Applying the boundary conditions, the constants are evaluated as
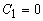 and and 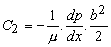 |
|
So, the solution is
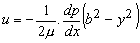 |
(25.13) |
which implies that the velocity profile is parabolic.
Average Velocity and Maximum Velocity
- To establish the relationship between the maximum velocity and average velocity in the channel, we analyze as follows
At y = 0, 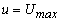 ; this yields ; this yields
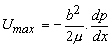 |
(25.14a) |
On the other hand, the average velocity,
Finally, 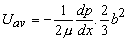 |
(25.14b) |
So, 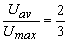 or or 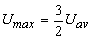 |
(25.14c) |
- The shearing stress at the wall for the parallel flow in a channel can be determined from the velocity gradient as
Since the upper plate is a "minus y surface", a negative stress acts in the positive x direction, i.e. to the right.
- The local friction coefficient, Cf is defined by
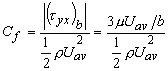 |
|
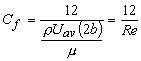 |
(25.14d) |
where 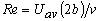 is the Reynolds number of flow based on average velocity and the channel height (2b). is the Reynolds number of flow based on average velocity and the channel height (2b).
- Experiments show that Eq. (25.14d) is valid in the laminar regime of the channel flow.
- The maximum
Reynolds number value corresponding to fully developed
laminar flow, for which a stable motion will persist, is
2300.
- In a reasonably careful experiment, laminar flow can be observed up to even Re = 10,000.
- But the value below which the flow will always remain laminar, i.e. the critical value of Re is 2300.
End of Lecture 25!
To start next lecture click next button or select from left-hand-side.
|
|