|
General Viscosity Law
Newton's viscosity law is
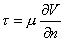 |
(24.1) |
where,
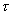 = Shear Stress, = Shear Stress,
n is the coordinate direction normal to the solid-fluid interface,
μ is the coefficient of viscosity, and
V is velocity.
The above law is valid for parallel flows.
Considering Stokes' viscosity law: shear stress is proportional to rate of shear strain so that
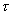 has two subscripts--- has two subscripts---
first subscript : denotes the direction of the normal to the plane on which the stress acts, while the
second subscript : denotes direction of the force which causes the stress. |
The expressions of Stokes' law of viscosity for normal stresses are
where
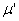 is a proportionality factor and it is related to the second coefficient of viscosity μ1 by the relationship is a proportionality factor and it is related to the second coefficient of viscosity μ1 by the relationship
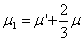 . .
We have already seen that the thermodyamic pressure is 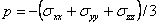
Now if we add the three equations 24.3(a),(b) and (c) , we obtain,
or
- For incompressible fluids,
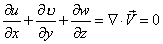
So, 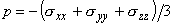 is satisfied eventually. This is known as Thermodynamic pressure. is satisfied eventually. This is known as Thermodynamic pressure.
- For compressible fluids, Stokes' hypothesis is
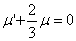 . .
- Invoking this to Eq. (24.4), will finally result in
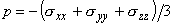 (same as for incompressible fluid). (same as for incompressible fluid).
- Interesting historical aspects of the Stoke's assumption
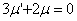 can be found in Truesdell can be found in Truesdell
 . .
- ----------------------------------------------------------------------------------------------------------------------------------------------------------------------
† Truesdell , C.A. "Stoke's Principle of Viscosity", Journal of Rational Mechanics and Analysis, Vol.1, pp.228-231,1952.
- ----------------------------------------------------------------------------------------------------------------------------------------------------------------------
- Generally, fluids obeying the ideal gas equation follow this hypothesis and they are called Stokesian fluids .
- The second coefficient of viscosity, μ1 has been verified to be negligibly small.
Substituting μ for 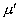 in 24.3a, 24.3b, 24.3c we obtain in 24.3a, 24.3b, 24.3c we obtain
In deriving the above stress-strain rate relationship, it was assumed that a fluid has the following properties
- Fluid is homogeneous and isotropic, i.e. the relation between components of stress and those of rate of strain is the same in all directions.
- Stress is a linear function of strain rate.
- The stress-strain relationship
will hold good irrespective of the orientation of the
reference coordinate system.
The stress components must reduce to the hydrostatic pressure "p" (typically thermodynamic pressure = hydrostatic pressure ) when all the gradients of velocities are zero.
|