Generation of Vortices Around a Wing

• The lift around an aerofoil is generated following Kutta-Joukowski theorem . Lift is a product of ρ , 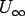and the circulation .

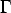• When the motion of a wing starts from rest, vortices are formed at the trailing edge.
  
• At the start, there is a velocity discontinuity at the trailing edge. This is eventual because near the trailing edge, the velocity at the bottom surface is higher than that at the top surface. This discrepancy in velocity culminates in the formation of vortices at the trailing edge.
  
• Figure 23.6(a) depicts the formation of starting vortex by impulsively moving aerofoil. However, the starting vortices induce a counter circulation as shown in Figure 23.6(b). The circulation around a path (ABCD) enclosing the wing and just shed (starting) vortex must be zero. Here we refer to Kelvin's theorem once again.

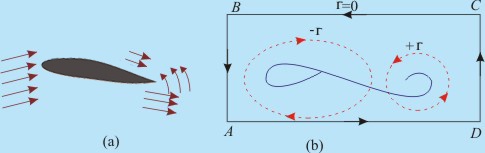
Fig 23.6    Vortices Generated when an Aerofoil Just Begins to Move

• Initially, the flow starts with the zero circulation around the closed path. Thereafter, due to the change in angle of attack or flow velocity, if a fresh starting vortex is shed, the circulation around the wing will adjust itself so that a net zero vorticity is set around the closed path.
  
• Real wings have finite span or finite aspect ratio (AR) λ , defined as

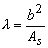(23.16)

where b is the span length, A_s is the plan form area as seen from the top..

• For a wing of finite span, the end conditions affect both the lift and the drag. In the leading edge region, pressure at the bottom surface of a wing is higher than that at the top surface. The longitudinal vortices are generated at the edges of finite wing owing to pressure differences between the bottom surface directly facing the flow and the top surface.

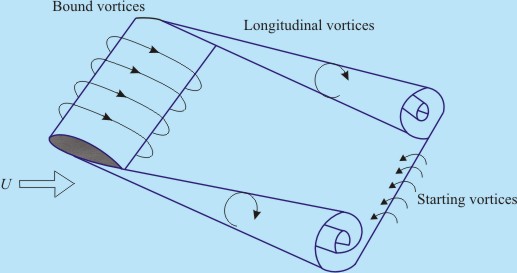
Fig 23.7    Vortices Around a Finite Wing

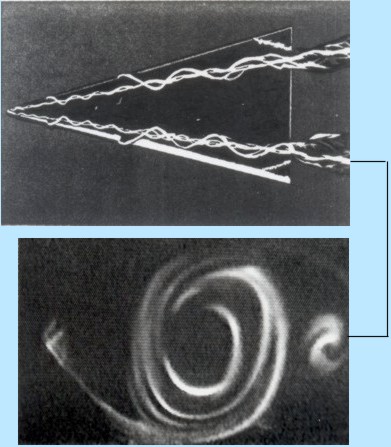
Fig 23.8   Generation of Longitudinal Vortices