|
Flow Around a Thin Aerofoil
- Thin aerofoil theory is based upon the superposition of uniform flow at infinity and a continuous distribution of clockwise free vortex on the camber line having circulation density
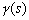 per unit length . per unit length .
- The circulation density
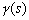 should be such that the resultant flow is tangent to the camber line at every point. should be such that the resultant flow is tangent to the camber line at every point.
- Since the slope of the camber line is assumed to be small,
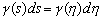 . The total circulation around the profile is given by . The total circulation around the profile is given by
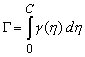 |
(23.13) |
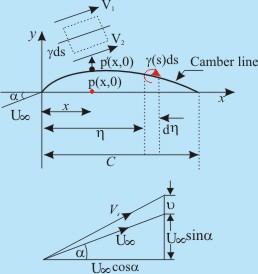
Fig 23.5 Flow Around Thin Aerofoil
A vortical motion of strength 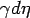 at x= at x= 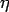 develops a velocity at the
point p which may be expressed as develops a velocity at the
point p which may be expressed as
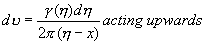
The total induced velocity in the upward direction at
point p due to the entire vortex distribution along the camber line is
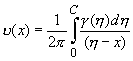 (23.14) (23.14)
For a small camber (having small
α), this expression is identically
valid for the induced velocity at point p' due to the vortex sheet of variable strength 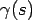 on the camber line. The resultant velocity due to on the camber line. The resultant velocity due to 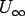 and v(x) must be tangential to the camber line so that the slope of a camber line may be expressed as and v(x) must be tangential to the camber line so that the slope of a camber line may be expressed as
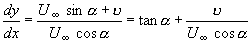
|
|
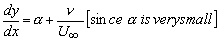 |
(23.15) |
From Eqs (23.14) and (23.15) we can write
Consider an element ds on the camber line. Consider a small rectangle (drawn with dotted line) around ds. The upper and lower sides of the rectangle are very close to each other and these are parallel to the camber line. The other two sides are normal to the camber line. The circulation along the rectangle is measured in clockwise direction as
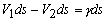 [normal component of velocity at the camber line should be zero] [normal component of velocity at the camber line should be zero] |
|
or 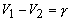 |
|
If the mean velocity in the tangential direction at the camber line is given by 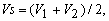 it can be rewritten as it can be rewritten as
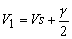 and and 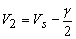 |
|
if v is very small 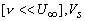 becomes equal to becomes equal to 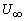 . The difference in velocity across the camber line brought about by the vortex sheet of variable strength . The difference in velocity across the camber line brought about by the vortex sheet of variable strength 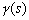 causes pressure difference and generates lift force. causes pressure difference and generates lift force. |