|
Classification of non-Newtonian fluids
- Many mathematical models are available to describe the nonlinear "shear-stress vs deformation-rate" relationship of non Newtonian fluids. But no general model can describe the constitutive equation ("shear stress vs rate of deformation" relationship) of all kinds of non-Newtonian fluids. However, the mathematical model for describing the mechanistic behaviour of a variety of commonly used non-Newtonian fluids is the Power-Law model which is also known as Ostwald-de Waele model (the name is after the scientist who proposed it). According to Ostwald-de Waele model
 |
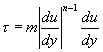(2.1) |
where m is known as the flow consistency index and n is the flow behavior index.
Hence viscosity for the Power-law fluids (as per Power Law model) can be described as:
μ =  |
(2.2) |
It can be observed from above that the viscosity of non-Newtonian fluid is function of deformation rate and is often termed as apparent or effective viscosity.
- When n = 1, m equals
 , the model identically satisfies Newtonian model as a special case.
When n < 1, the model is
valid for pseudoplastic fluids,
such as gelatine, blood, milk etc.
When n > 1, the model is
valid for dilatant fluids,
such as sugar in water, aqueous suspension of rice starch
etc.
- There are some substances which require a yield stress for the deformation rate (i.e. the flow) to be established, and hence their constitutive equations do not pass through the origin thus violating the basic definition of a fluid. They are termed as Bingham plastic. For an ideal Bingham plastic, the shear stress- deformation rate relationship is linear.
|
