|
Stagnation Pressure
- The stagnation pressure at a point in
a fluid flow is the pressure which could result if the fluid
were brought to rest isentropically.
- The word isentropically implies
the sense that the entire kinetic energy of a fluid particle
is utilized to increase its pressure only. This is possible
only in a reversible adiabatic process known as isentropic
process.
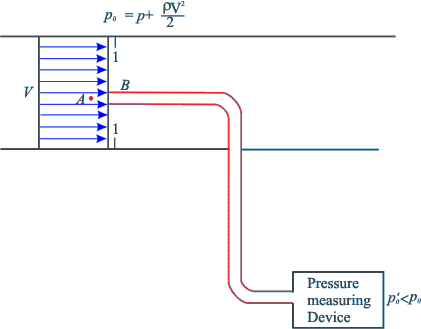
Fig 16.2 Measurement
of Stagnation Pressure
- Let us consider the flow of fluid through
a closed passage (Fig. 16.2). At Sec. l-l let the velocity
and static pressure of the fluid be uniform. Consider a
point A on that section just in front of which a right angled
tube with one end facing the flow and the other end
closed is placed.
- When equilibrium is attained, the fluid
in the tube will be at rest, and the pressure at any point
in the tube including the point B will be more than that
at A where the flow velocity exists.
- By the application of Bernoulli’s
equation between the points B and A, in consideration of
the flow to be inviscid and incompressible, we have,
 |
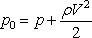(16.6) |
where p and V are the pressure and velocity respectively at the point A at
Sec. I-I, and p0 is the pressure at B which, according to the definition, refers
to the stagnation pressure at point A.
- It is found from Eq. (16.6) that the
stagnation pressure p0 consists of two terms,
the static pressure, p
and the term ρV2/2 which
is known as dynamic pressure. Therefore
Eq. (16.6) can be written for a better understanding as
 |
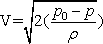(16.7) |
- Therefore, it appears from Eq.(16.7), that from a measurement of both static and stagnation
pressure in a flowing fluid, the velocity of flow can be
determined.
- But it is difficult to measure the stagnation
pressure in practice for a real fluid due to friction. The
pressure
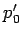in the stagnation tube indicated by any pressure measuring
device (Fig. 16.2) will always be less than p0,
since a part of the kinetic energy will be converted into
intermolecular energy due to fluid friction). This is taken
care of by an empirical factor C in determining the velocity
from Eq. (16.7) as
 |
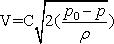(16.8) |
|
