Chapter 5 : Applications of Equations of Motion and Mechanical Energy
Lecture 16 :


Hydrostatic, Hydrodynamic, Static and Total Pressure

  • Let us consider a fluid flowing through a pipe of varying cross sectional area. Considering two points A and B as shown in Figure 16.1(c), such that A and B are at a height ZA and ZB respectively from the datum.

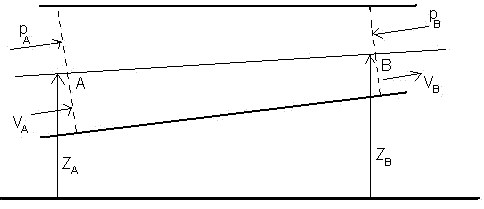
Figure 16.1 (c)

  • If we consider the fluid to be stationary, then, 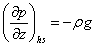    where the subscript ‘hs’ represents the hydrostatic case.

So,   pAhs - pBhs = ρg( ZB–ZA)    

 

 (16.1)

where pAhs is the hydrostatic pressure at A and pBhs is the hydrostatic pressure at B.

  • Thus, from above we can conclude that the Hydrostatic pressure at a point in a fluid is the pressure acting at the point when the fluid is at rest or pressure at the point due to weight of the fluid above it.

  • Now if we consider the fluid to be moving, the pressure at a point can be written as a sum of two components, Hydrodynamic and Hydrostatic.
pA = pAhs + pAhd     (16.2)

where pAhs is the hydrostatic pressure at A and pAhd is the hydrodynamic pressure at A.

  • Using equation (16.2) in Bernoulli's equation between points A and B.
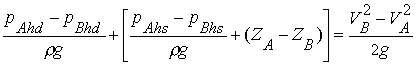(16.3)

 

From equation (16.1), the terms within the square bracket cancel each other.

Hence,

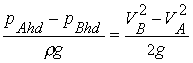(16.4)
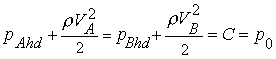(16.5)

                                                

  • Equations (16.4) and (16.5) convey the following. The pressure at a location has both hydrostatic and hydrodynamic components. The difference in kinetic energy arises due to hydrodynamic components only.

  • In a frictionless flow, the sum of flow work due to hydrodynamic pressure and the kinetic energy is conserved. Such conservation shall apply to the entire flow field if the flow is irrotational.

  • The hydrodynamic component is often called static pressure and the velocity term, dynamic pressure. The sum of two, p0 is known as total pressure. This is conserved in isentropic, irrotational flow.