Conservation of Energy

The principle of conservation of energy for a control mass system is described by the first law of thermodynamics

Heat Q added to a control mass system- the work done W by the control mass system = change in its internal energy E

The internal energy depends only upon the initial and final states of the system. It can be written in the form of the equation as

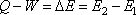(13.1a)

Equation (13.1a) can be expressed on the time rate basis as

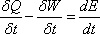(13.1b)

Where δQ and δW are the amount of heat added and work done respectively during a time interval of δt. To develop the analytical statement for the conservation of energy of a control volume, the Eq. (10.10) is used with N = E (the internal energy) and η = e (the internal energy per unit mass) along with the Eq. (13.1b). This gives

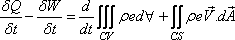(13.2)

The Eq. (13.2) is known as the general energy equation for a control volume.

The first term on the right hand side of the equation is the time rate of increase in the internal energy within a control volume and the second term is the net rate of energy efflux from the control volume.

Different forms of energy associated with moving fluid elements comprising a control volume are -

1. Potential energy
The concept of potential energy in a fluid is essentially the same as that of a solid mass. The potential energy of a fluid element arises from its existence in a conservative body force field. This field may be a magnetic, electrical, etc. In the absence of any of such external force field, the earth’s gravitational effect is the only cause of potential energy. If a fluid mass m is stored in a reservoir and its C.G. is at a vertical distance z from an arbitrary horizontal datum plane, then the potential energy is mgz and the potential energy per unit mass is gz. The arbitrary datum does not play a vital role since the difference in potential energy, instead of its absolute value, is encountered in different practical purposes.

2. Kinetic Energy
If a quantity of a fluid of mass m flows with a velocity V, being the same throughout its mass, then the total kinetic energy is mV²/2 and the kinetic energy per unit mass is V²/2. For a stream of real fluid, the velocities at different points will not be the same. If V is the local component of velocity along the direction of flow for a fluid flowing through an open channel or closed conduit of cross-sectional area A, the total kinetic energy at any section is evaluated by summing up the kinetic energy flowing through differential areas as

The average velocity at a cross-section in a flowing stream is defined on the basis of volumetric flow rate as,

The kinetic energy per unit mass of the fluid is usually expressed as 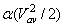where α is known as the kinetic energy correction factor.
Therefore, we can write

Hence,   

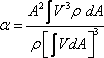(13.3a)

For an incompressible flow,

(13.3b)

3. Intermolecular Energy
The intermolecular energy of a substance comprises the potential energy and kinetic energy of the molecules. The potential energy arises from intermolecular forces. For an ideal gas, the potential energy is zero and the intermolecular energy is, therefore, due to only the kinetic energy of molecules. The kinetic energy of the molecules of a substance depends on its temperature.

4. Flow Work

Flow work is the work done by a fluid to move against pressure.
For a flowing stream, a layer of fluid at any cross-section has to push the adjacent neighboring layer at its downstream in the direction of flow to make its way through and thus does work on it. The amount of work done can be calculated by considering a small amount of fluid mass A₁ ρ₁ dx to cross the surface AB from left to right (Fig. 13.1). The work done by this mass of fluid then becomes equal to p₁ A₁ dx and thus the flow work per unit mass can be expressed as

(where p₁ is the pressure at section AB (Fig 13.1)

Fig 13.1   Work done by a fluid to flow against pressure

Therefore the flow work done per unit mass by a fluid element entering the control volume ABCDA (Fig. 13.1) is p₁ /ρ₁ Similarly, the flow work done per unit mass by a fluid element leaving the control volume across the surface CD is p₂/ρ₁

Important- In introducing an amount of fluid inside the control volume, the work done against the frictional force at the wall can be shown to be small as compared to the work done against the pressure force, and hence it is not included in the flow work.

Although ’flow work’ is not an intrinsic form of energy, it is sometimes referred to as ’pressure energy’ from a view point that by virtue of this energy a mass of fluid having a pressure p at any location is capable of doing work on its neighboring fluid mass to push its way through.