|
A Control Volume Approach for the Derivation of Euler’s Equation
Euler’s equations of motion can also be derived by the use of the momentum theorem for a control volume.
Derivation
In a fixed x, y, z axes (the rectangular
cartesian coordinate system), the parallelopiped which was
taken earlier as a control mass system is now considered as
a control volume (Fig. 12.4).
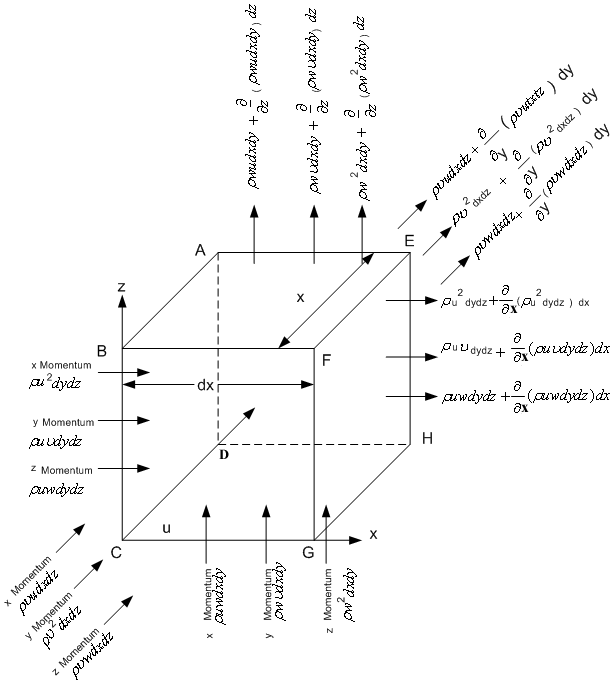
Fig 12.4 A
Control Volume used for the derivation of Euler's Equation
We can define the velocity vector 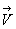 and the body force per unit volume and the body force per unit volume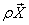 as as
The rate of x momentum influx to the control volume through the face ABCD is equal to ρu2 dy dz. The rate of x momentum efflux from the control volume through the face EFGH equals 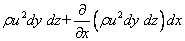
Therefore the rate of net efflux of x momentum from the control volume due to the faces perpendicular to the x direction (faces ABCD and EFGH) =
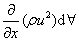 where, where,
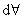 , the elemental volume = dx dy dz. , the elemental volume = dx dy dz.
Similarly,
The rate of net efflux of x momentum due to the faces perpendicular to the y direction (face BCGF and ADHE)
=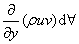
The rate of net efflux of x momentum due to the faces perpendicular to the z direction (faces DCGH and ABFE) =
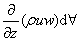
Hence, the net rate of x momentum efflux from the control volume becomes The time rate of increase in x momentum in the control volume can be written as
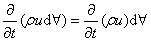 (Since, (Since,
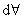 , by the definition of control volume, is invariant with time) , by the definition of control volume, is invariant with time)
Applying the principle of momentum conservation to a control volume (Eq. 4.28b), we get
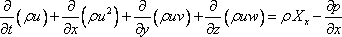 |
(12.11a) |
The equations in other directions y and z can be obtained in a similar way by considering the y momentum and z momentum fluxes through the control volume as
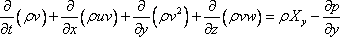 |
(12.11b) |
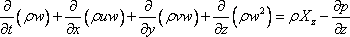 |
(12.11c) |
The typical form of Euler’s
equations given by Eqs (12.11a), (12.11b) and (12.11c) are
known as the conservative forms.
End of Lecture 12!
To start next lecture click next button or select from left-hand-side.
|
|