Euler’s Equation along a Streamline

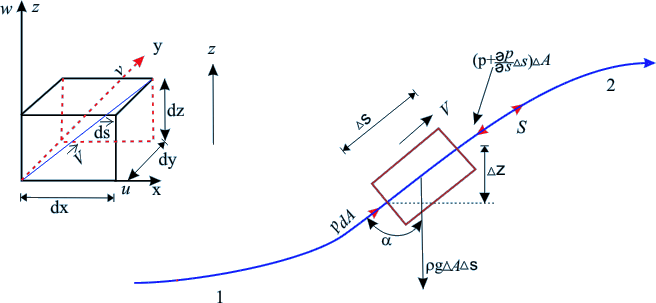
Fig 12.3  Force Balance on a Moving Element Along a Streamline

Derivation
Euler’s equation along a streamline is derived by applying Newton’s second law of motion to a fluid element moving along a streamline. Considering gravity as the only body force component acting vertically downward (Fig. 12.3), the net external force acting on the fluid element along the directions can be written as

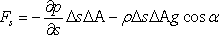(12.8)

where ∆A is the cross-sectional area of the fluid element. By the application of Newton’s second law of motion in s direction, we get    

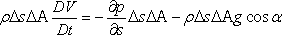(12.9)

From geometry we get

Hence, the final form of Eq. (12.9) becomes

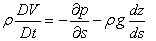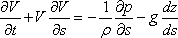	(12.10)

Equation (12.10) is the Euler’s equation along a streamline.

Let us consider 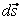along the streamline so that

Again, we can write from Fig. 12.3

The equation of a streamline is given by

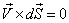or, 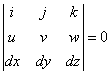     which finally leads to

          
Multiplying Eqs (12.7a), (12.7b) and (12.7c) by dx, dy and dz respectively and then substituting the above mentioned equalities, we get

Adding these three equations, we can write

=

=  

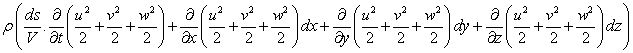
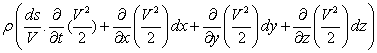
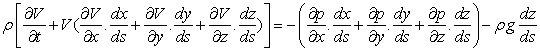
Hence,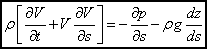    

This is the more popular form of Euler's equation because the velocity vector in a flow field is always directed along the streamline.