|
Euler’s Equation: The Equation of Motion of an Ideal Fluid
This section is not a mandatory requirement. One can skip this section (if he/she does not like to spend time on Euler's equation) and go directly to Steady Flow Energy Equation.
Using the Newton's second law of motion the relationship between the velocity and pressure field for a flow of an inviscid fluid can be derived. The resulting equation, in its differential form, is known as Euler’s Equation. The equation is first derived by the scientist Euler.
Derivation:
Let us consider an elementary parallelopiped
of fluid element as a control mass system in a frame of rectangular
cartesian coordinate axes as shown in Fig. 12.3. The external
forces acting on a fluid element are the body forces and the
surface forces.
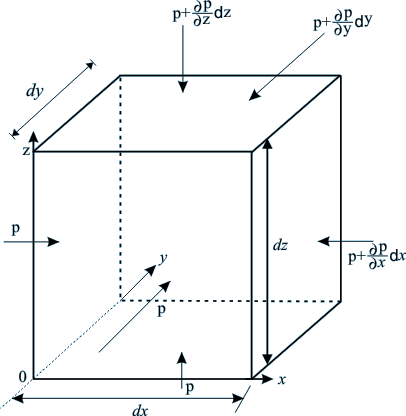
Fig 12.2 A
Fluid Element appropriate to a Cartesian Coordinate System
used for the derivation of Euler's Equation
Let Xx, Xy,
Xz be the components of body forces acting per
unit mass of the fluid element along the coordinate axes x,
y and z respectively. The body forces arise due to external
force fields like gravity, electromagnetic field, etc., and
therefore, the detailed description of Xx, Xy
and Xz are provided by the laws of physics describing
the force fields. The surface forces for an inviscid fluid
will be the pressure forces acting on different surfaces as
shown in Fig. 12.3. Therefore, the net forces acting on the
fluid element along x, y and z directions can be written as
Since each component of the force can be expressed as the rate of change of momentum in the respective directions, we have
s the mass of a control mass system does
not change with time,
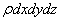 is constant with time and can be taken common.
Therefore we can write Eqs (12.5a to 12.5c) as is constant with time and can be taken common.
Therefore we can write Eqs (12.5a to 12.5c) as
Expanding the material accelerations
in Eqs (12.6a) to (12.6c) in terms of their respective temporal
and convective components, we get
The Eqs (12.7a, 12.7b, 12.7c)
are valid for both incompressible and compressible flow. By
putting u = v = w = 0, as a
special case, one can obtain the equation of hydrostatics
.
Equations (12.7a), (12.7b), (12.7c) can be put into a single
vector form as
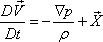 |
(12.7d) |
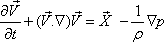 |
(12.7e) |
where 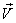 the velocity vector and the body force vector per unit volume the velocity vector and the body force vector per unit volume
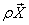 are defined as are defined as
|
Equation (12.7d) or
(12.7e) is the well known Euler’s equation
in vector form,
while Eqs (12.7a) to (12.7c) describe the Euler’s
equations in a rectangular Cartesian coordinate system.
|
|