Cavitation in reaction turbines
If the pressure of a liquid in course of its flow becomes equal to its vapour pressure at the existing temperature, then the liquid starts boiling and the pockets of vapour are formed which create vapour locks to the flow and the flow is stopped. The phenomenon is known as cavitation. To avoid cavitation, the minimum pressure in the passage of a liquid flow, should always be more than the vapour pressure of the liquid at the working temperature. In a reaction turbine, the point of minimum pressure is usually at the outlet end of the runner blades, i.e at the inlet to the draft tube. For the flow between such a point and the final discharge into the trail race (where the pressure is atmospheric), the Bernoulli's equation can be written, in consideration of the velocity at the discharge from draft tube to be negligibly small, as
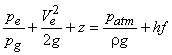 |
(31.1) |
where, 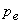 and and 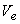 represent the static pressure and velocity of the liquid at the outlet of the runner (or at the inlet to the draft tube). The larger the value of represent the static pressure and velocity of the liquid at the outlet of the runner (or at the inlet to the draft tube). The larger the value of 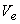 , the smaller is the value of , the smaller is the value of 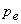 and the cavitation is more likely to occur. The term and the cavitation is more likely to occur. The term 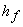 in Eq. (31.1) represents the loss of head due to friction in the draft tube and z is the height of the turbine runner above the tail water surface. For cavitation not to occur in Eq. (31.1) represents the loss of head due to friction in the draft tube and z is the height of the turbine runner above the tail water surface. For cavitation not to occur 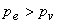 where where 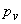 is the vapour pressure of the liquid at the working temperature. is the vapour pressure of the liquid at the working temperature.
An important parameter in the context of cavitation is the available suction head (inclusive of both static and dynamic heads) at exit from the turbine and is usually referred to as the net positive suction head 'NPSH' which is defined as
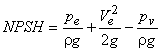 |
(31.2) |
with the help of Eq. (31.1) and in consideration of negligible frictional losses in the draft tube 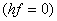 , Eq. (31.2) can be written as , Eq. (31.2) can be written as
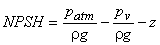 |
(31.3) |
A useful design parameter 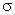 known as Thoma's Cavitation Parameter (after the German Engineer Dietrich Thoma, who first introduced the concept) is defined as known as Thoma's Cavitation Parameter (after the German Engineer Dietrich Thoma, who first introduced the concept) is defined as
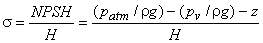 |
(31.4) |
For a given machine, operating at its design condition, another useful parameter 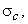 known as critical cavitaion parameter is define as known as critical cavitaion parameter is define as
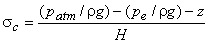 |
(31.5) |
Therefore, for cavitaion not to occur 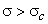 (since, (since, 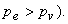
If either z or H is increased, 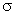 is reduced. To determine whether cavitation is likely to occur in a particular installation, the value is reduced. To determine whether cavitation is likely to occur in a particular installation, the value 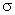 of may be calculated. When the value of of may be calculated. When the value of 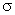 is greater than the value of is greater than the value of 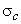 for a particular design of turbine cavitation is not expected to occur. for a particular design of turbine cavitation is not expected to occur.
In practice, the value of 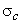 is used to determine the maximum elevation of the turbine above tail water surface for cavitation to be avoided. The parameter of increases with an increase in the specific speed of the turbine. Hence, turbines having higher specific speed must be installed closer to the tail water level. is used to determine the maximum elevation of the turbine above tail water surface for cavitation to be avoided. The parameter of increases with an increase in the specific speed of the turbine. Hence, turbines having higher specific speed must be installed closer to the tail water level. |