More
About Energy Transfer in Turbomachines
Equation (1.7) can be better explained
by demonstrating a steady flow through a container
having uniform angular velocity 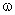 as
shown in Fig.1.3b. The centrifugal force on an infinitesimal
body of a fluid of mass dm at radius r gives
rise to a pressure differential dp across
the thickness dr of the body in a manner
that a differential force of dpdA acts
on the body radially inward. This force, in fact,
is the centripetal force responsible for the rotation
of the fluid element and thus becomes equal to the
centrifugal force under equilibrium conditions in
the radial direction. Therefore, we can write as
shown in Fig.1.3b. The centrifugal force on an infinitesimal
body of a fluid of mass dm at radius r gives
rise to a pressure differential dp across
the thickness dr of the body in a manner
that a differential force of dpdA acts
on the body radially inward. This force, in fact,
is the centripetal force responsible for the rotation
of the fluid element and thus becomes equal to the
centrifugal force under equilibrium conditions in
the radial direction. Therefore, we can write
with dm = dA dr
ρ where
ρ is the density of the fluid, it becomes
For a reversible flow (flow without friction) between two points, say, 1 and 2, the work done per unit mass of the fluid (i.e., the flow work) can be written as
The work is, therefore, done on or by the fluid element due to its displacement from radius 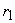 to radius to radius 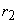 and hence becomes equal to the energy held or lost by it. Since the centrifugal force field is responsible for this energy transfer, the corresponding head (energy per unit weight) and hence becomes equal to the energy held or lost by it. Since the centrifugal force field is responsible for this energy transfer, the corresponding head (energy per unit weight) 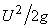 is termed as centrifugal head. The transfer of energy due to a change in centrifugal head is termed as centrifugal head. The transfer of energy due to a change in centrifugal head 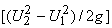 causes a change in the static head of the fluid. causes a change in the static head of the fluid.
The third term represents a change in the static head due to a change in fluid velocity relative to the rotor. This is similar to what happens in case of a flow through a fixed duct of variable cross-sectional area. Regarding the effect of flow area on fluid velocity 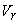 relative to the rotor, a converging passage in the direction of flow through the rotor increases the relative velocity relative to the rotor, a converging passage in the direction of flow through the rotor increases the relative velocity 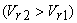 and hence decreases the static pressure. This usually happens in case of turbines. Similarly, a diverging passage in the direction of flow through the rotor decreases the relative velocity and hence decreases the static pressure. This usually happens in case of turbines. Similarly, a diverging passage in the direction of flow through the rotor decreases the relative velocity 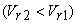 and increases the static pressure as occurs in case of pumps and compressors. and increases the static pressure as occurs in case of pumps and compressors.
The fact that the second and third terms of Eq. (1.7) correspond to a change in static head can be demonstrated analytically by deriving Bernoulli's equation in the frame of the rotor.
In a rotating frame, the momentum equation for the flow of a fluid, assumed "inviscid" can be written as
where 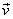 is the fluid velocity relative to the coordinate frame rotating with an angular velocity is the fluid velocity relative to the coordinate frame rotating with an angular velocity 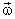 . .
We assume that the flow is steady in the rotating frame so that 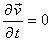 . We choose a cylindrical coordinate system . We choose a cylindrical coordinate system 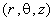 with z-axis along the axis of rotation. Then the momentum equation reduces to with z-axis along the axis of rotation. Then the momentum equation reduces to
where  and and 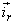 are the unit vectors along z and r direction respectively. Let are the unit vectors along z and r direction respectively. Let 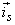 be a unit vector in the direction of be a unit vector in the direction of 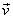 and s be a coordinate along the stream line. Then we can write and s be a coordinate along the stream line. Then we can write
|