However, for an axisymmetric flow, this does not result in any net radial force on the rotor. In case of a non uniform flow distribution over the periphery of the rotor in practice, a change in momentum in radial direction may result in a net radial force which is carried as a journal load. The tangential component  only has an effect on the angular motion of the rotor. In consideration of the entire fluid body within the rotor as a control volume, we can write from the moment of momentum theorem only has an effect on the angular motion of the rotor. In consideration of the entire fluid body within the rotor as a control volume, we can write from the moment of momentum theorem
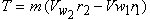 |
(1.1) |
where T is the torque exerted by the rotor on the moving fluid, m is the mass flow rate of fluid through the rotor. The subscripts 1 and 2 denote values at inlet and outlet of the rotor respectively. The rate of energy transfer to the fluid is then given by
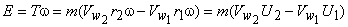 |
(1.2) |
where  is
the angular velocity of the rotor and is
the angular velocity of the rotor and 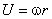 which
represents the linear velocity of the rotor. Therefore which
represents the linear velocity of the rotor. Therefore  and and  are
the linear velocities of the rotor at points 2 (outlet
) and 1 (inlet) respectively (Fig. 1.2). The Eq,
(1.2) is known as Euler's equation in relation to
fluid machines. The Eq. (1.2) can be written in terms
of head gained 'H' by the fluid as are
the linear velocities of the rotor at points 2 (outlet
) and 1 (inlet) respectively (Fig. 1.2). The Eq,
(1.2) is known as Euler's equation in relation to
fluid machines. The Eq. (1.2) can be written in terms
of head gained 'H' by the fluid as
In usual convention relating to fluid machines, the head delivered by the fluid to the rotor is considered to be positive and vice-versa. Therefore, Eq. (1.3) written with a change in the sign of the right hand side in accordance with the sign convention as
 |
(1.4)
|
Components
of Energy Transfer It is worth mentioning
in this context that either of the Eqs. (1.2)
and (1.4) is applicable regardless of changes
in density or components of velocity in other
directions. Moreover, the shape of the path taken
by the fluid in moving from inlet to outlet is
of no consequence. The expression involves only
the inlet and outlet conditions. A rotor, the
moving part of a fluid machine, usually consists
of a number of vanes or blades mounted on a circular
disc. Figure 1.3a shows the velocity triangles
at the inlet and outlet of a rotor. The inlet
and outlet portions of a rotor vane are only
shown as a representative of the whole rotor.
| Fig
1.3 (a) |
Velocity triangles for a generalised rotor vane |
| Fig
1.3 (b) |
Centrifugal effect in a flow of fluid with rotation |
Vector diagrams of velocities at inlet and outlet correspond to two velocity triangles, where  is the velocity of fluid relative to the rotor and is the velocity of fluid relative to the rotor and  are the angles made by the directions of the absolute velocities at the inlet and outlet respectively with the tangential direction, while are the angles made by the directions of the absolute velocities at the inlet and outlet respectively with the tangential direction, while 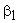 and and  are the angles made by the relative velocities with the tangential direction. The angles are the angles made by the relative velocities with the tangential direction. The angles  and and  should match with vane or blade angles at inlet and outlet respectively for a smooth, shockless entry and exit of the fluid to avoid undersirable losses. Now we shall apply a simple geometrical relation as follows: should match with vane or blade angles at inlet and outlet respectively for a smooth, shockless entry and exit of the fluid to avoid undersirable losses. Now we shall apply a simple geometrical relation as follows:
From the inlet velocity triangle,
or, 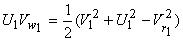 |
(1.5) |
Similarly from the outlet velocity triangle.
or,  |
(1.6) |
Invoking the expressions of 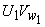 and and  in Eq. (1.4), we get H (Work head, i.e. energy per unit weight of fluid, transferred between the fluid and the rotor as) as in Eq. (1.4), we get H (Work head, i.e. energy per unit weight of fluid, transferred between the fluid and the rotor as) as
The Eq (1.7) is an important form of the Euler's equation relating to fluid machines since it gives the three distinct components of energy transfer as shown by the pair of terms in the round brackets. These components throw light on the nature of the energy transfer. The first term of Eq. (1.7) is readily seen to be the change in absolute kinetic energy or dynamic head of the fluid while flowing through the rotor. The second term of Eq. (1.7) represents a change in fluid energy due to the movement of the rotating fluid from one radius of rotation to another.
|