Example on Assembly of Stiffness Matrix and Force Vector As an example, consider the mesh of 6 elements (N = 6) and 7 nodes, shown in Fig. 6.4.
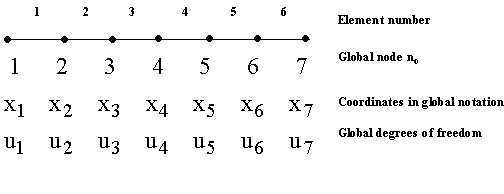
Figure 6.4 Mesh with 6 elements
The connectivity matrix for this mesh can be written as:
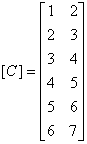 . . |
(6.42) |
Let
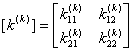 , , |
(6.43) |
and
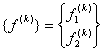 |
(6.44) |
be the element stiffness matrix and the element force vector of the elements 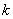 =1,2,3,4,5,6. =1,2,3,4,5,6.
Consider the element 1, i.e. 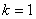 . Note that . Note that
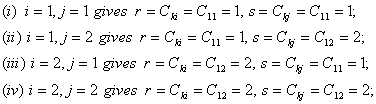 |
(6.45) |
Then as per equation (6.36), components of the stiffness matrix of the element 1, i.e. of 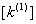 , occupy the following locations in the expanded matrix , occupy the following locations in the expanded matrix 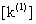 : :
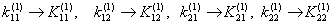 |
(6.46) |
Similarly, as per equation (6.37), components of the force vector of the element 1, i.e. of 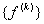 , occupy the following locations in the expanded vector , occupy the following locations in the expanded vector 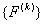 : :
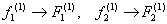 |
(6.47) |
The remaining components of the expanded matrix 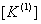 and the expanded vector and the expanded vector 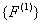 are zero. Thus, the matrix are zero. Thus, the matrix 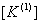 becomes: becomes:
 . . |
(6.48) |
and the vector 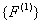 becomes: becomes:
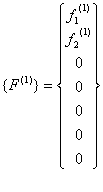 |
(6.49) |
Similarly, we obtain the expanded versions of the element stiffness matrix 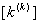 and the element force vector and the element force vector 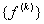 for the remaining elements, i.e. for for the remaining elements, i.e. for 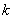 = 2,3,4,5,6. It can easily be verified that, for the 3 rd element (i.e. for = 2,3,4,5,6. It can easily be verified that, for the 3 rd element (i.e. for 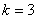 ), the expanded matrix ), the expanded matrix 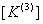 and the expanded vector and the expanded vector 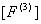 are: are:
 |
(6.50a) |
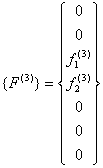 |
(6.50b) |
This completes the first step.
In the 2nd step, we add all the expanded matrices and vectors. Thus, equation (6.38) gives the following expression for the global stiffness matrix:
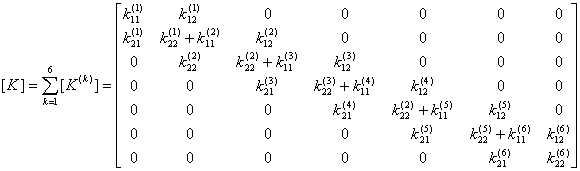 |
(6.51) |
Similarly, the sum of the expanded force vector becomes:
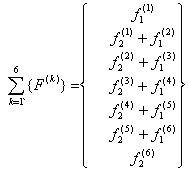 |
(6.52) |
However, before we get the global force vector 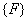 , we need to add the vector , we need to add the vector 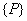 to the above expression. Since to the above expression. Since 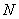 (no. of elements) = 6, the (no. of elements) = 6, the 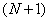 -th component, i.e. the 7-th component of the vector -th component, i.e. the 7-th component of the vector 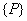 will be will be 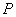 . The remaining components will be zero as per equation (6.41). Thus, . The remaining components will be zero as per equation (6.41). Thus, 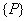 becomes: becomes:
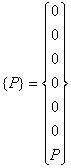 |
(6.53) |
Substituting the expressions (6.52) and (6.53) in equation (6.39), we get the following expression for the global force vector 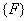 : :
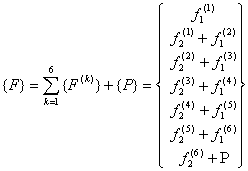 |
(6.54) |
Now, as in section 6.3, assume that 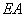 and and 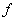 (distributed force) are constant for the entire bar. Further, assume that the length (distributed force) are constant for the entire bar. Further, assume that the length 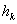 of each element is constant. Let us denote it by h . Then of each element is constant. Let us denote it by h . Then
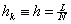 |
(6.55) |
Then, equation (6.32) implies that the element stiffness matrix 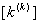 is identical for each element and is given by is identical for each element and is given by
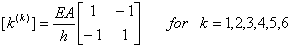 |
(6.56) |
Similarly, equation (6.33) implies that the element force vector 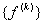 is identical for each element and is given by is identical for each element and is given by
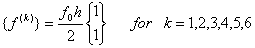 |
(6.57) |
Substituting the expression (6.56) in equation (6.51), we get

 |
(6.58) |
Further, substituting the expression (6.57) in equation (6.54), we get
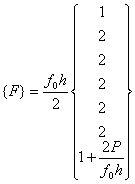 |
(6.59) |
In actual calculations, the assembly procedure is appropriately modified to reduce the computational time and storage requirements. When, the number of elements is large, storing of the expanded matrices and vectors for each element needs a lot of storage requirement. Therefore, the process is modified as follows:
- Once the expanded version
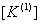 of the element stiffness matrix of the first element of the element stiffness matrix of the first element  is obtained, the element stiffness matrices of other elements are not expanded. is obtained, the element stiffness matrices of other elements are not expanded.
- Instead, the locations of the components of the stiffness matrix
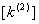 of the element two of the element two 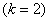 are determined using equation (6.36). are determined using equation (6.36).
- From the connectivity (6.34), it is easy to see that
 |
(6.60) |
|