Assembly of Stiffness Matrix and Force Vector
After the evaluation of element stiffness matrix and element force vector for all the elements, these quantities need to be " assembled " to get the global stiffness matrix and global force vector. As stated at the end of section 6.2, this procedure has two steps:
- Expansion of the element stiffness matrix and element force vector to the full size.
- Addition of the expanded matrices and vectors over all the elements. At this stage, the second term of the expression for
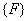 (equation 6.8) also needs to be added. (equation 6.8) also needs to be added.
Let us first discuss the first step. Note that equations (6.25) and (6.26) are the expressions for the element stiffness matrix 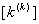 and the element force vector and the element force vector 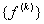 while equations (6.21) and (6.22) are the expressions for their expanded versions while equations (6.21) and (6.22) are the expressions for their expanded versions 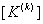 and and 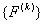 . When we compare equations (6.25) with (6.21), we observe that (1,1) component of . When we compare equations (6.25) with (6.21), we observe that (1,1) component of 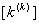 occupies the position occupies the position 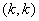 of the expanded matrix of the expanded matrix 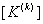 . This is because . This is because 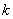 is the global number of the local node 1 of the element k. Thus, the first step involves: is the global number of the local node 1 of the element k. Thus, the first step involves:
- Choose the component
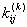 , , 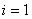 , , 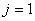
- Find the global number of the local nodes
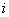 and and 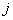 of the element of the element 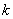 . Let they be . Let they be 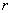 and and 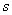 respectively. respectively.
- Then the component
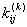 occupies the location in occupies the location in 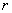 -th row and s -th column of the expanded matrix -th row and s -th column of the expanded matrix 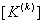 . Thus, the component . Thus, the component 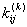 goes to the location goes to the location 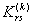 in the expanded matrix. in the expanded matrix.
- Repeat the steps (i)-(iii) for the other values of
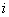 and and 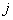 . The remaining components of . The remaining components of 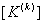 are made zero. are made zero.
The first step can be expressed mathematically by introducing a matrix 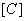 , called as the connectivity matrix , which relates the local and global numbering systems. The number of rows in the connectivity matrix is equal to the number of elements and the number of columns is equal to the number of nodes per element. Thus, the row index of , called as the connectivity matrix , which relates the local and global numbering systems. The number of rows in the connectivity matrix is equal to the number of elements and the number of columns is equal to the number of nodes per element. Thus, the row index of 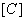 denotes the element number and the column index of denotes the element number and the column index of 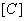 represents the local node number. The elements of represents the local node number. The elements of 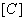 are the corresponding global node numbers. Thus, for the mesh of Fig. 6.1, the connectivity matrix becomes are the corresponding global node numbers. Thus, for the mesh of Fig. 6.1, the connectivity matrix becomes
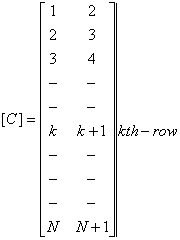 |
(6.34) |
The first row of the connectivity matrix contains the global numbers of the first and second local nodes of element 1. The global numbers corresponding to the first and second local nodes of element 2 are written in the second row. Continuing in this way, the global numbers of the first and second local nodes of element 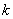 appear in the appear in the 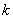 -th row. The last row contains the global numbers associated with the first and second local nodes of the last, i.e. -th row. The last row contains the global numbers associated with the first and second local nodes of the last, i.e. 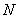 -th element. The expression (6.34), in the index notation, can be expressed as -th element. The expression (6.34), in the index notation, can be expressed as
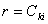 |
(6.35) |
It means the global number 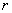 of the local node of the local node 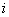 of the element of the element 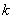 is obtained as the value of the component of the connectivity matrix in is obtained as the value of the component of the connectivity matrix in 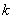 -th row and -th row and 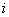 -th column. As an example, consider the case of -th column. As an example, consider the case of 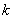 = 3 and = 3 and 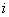 = 2. The expression (6.35) gives = 2. The expression (6.35) gives 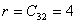 . This means 4 is the global number of the second local node of the element 3. This can be verified from Fig. 6.1. . This means 4 is the global number of the second local node of the element 3. This can be verified from Fig. 6.1.
Now, the first step of the assembly procedure can be expresses as follows. The expanded matrix 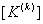 is obtained from the element stiffness matrix is obtained from the element stiffness matrix 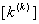 by the relation: by the relation:
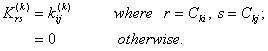 |
(6.36) |
Similarly, to obtain the expanded vector 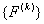 from the element force vector from the element force vector 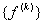 , we use the relation: , we use the relation:
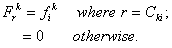 |
(6.37) |
Thus, we use the following procedure:
- Choose the component
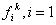
- Find the global number of the local node
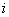 from the connectivity matrix. Let it be from the connectivity matrix. Let it be 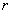 . .
- Then, the component
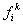 goes to the location goes to the location 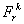 of the expanded matrix. of the expanded matrix.
- Repeat the steps (i)-(iii) for the other values of
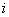 . The remaining components of . The remaining components of 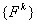 are made zero. are made zero.
The second-step is straight-forward. After obtaining the expanded versions of the element stiffness matrix and the element force vector for all the elements, they are added as follows:
 , , |
(6.38) |
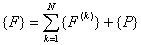 |
(6.39) |
The matrix 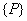 corresponds to the second term of equation (6.8). Note that, the only basis function which is nonzero at corresponds to the second term of equation (6.8). Note that, the only basis function which is nonzero at 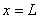 is is 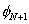 . Further, it's value at . Further, it's value at 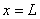 is 1. Thus is 1. Thus

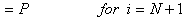 |
(6.40) |
Therefore, the vector {P} can be written as
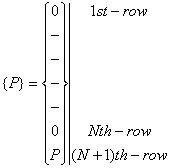 |
(6.41) |
|