Expressions for Element Stiffness Matrix and Force Vector
Now, we shall determine the row and column numbers of the matrix equation (5.14) to which the 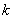 -th element makes the contribution. For this purpose, consider equation (5.13): -th element makes the contribution. For this purpose, consider equation (5.13):
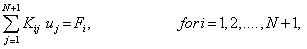 |
(6.6) |
where the expressions for the stiffness matrix 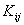 and the force vector and the force vector 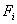 are given by equations (5.11) and (5.12): are given by equations (5.11) and (5.12):
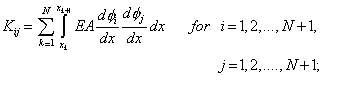 |
(6.7) |
and
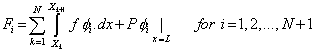 |
(6.8) |
The above expression can be written as
 |
(6.9) |
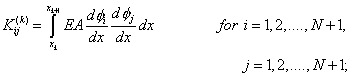 |
(6.10) |
and
 |
(6.11) |
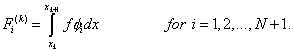 |
(6.12) |
Note th at 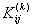 and and 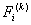 represent the contributions of the represent the contributions of the 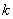 -th element to the stiffness matrix -th element to the stiffness matrix 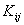 and the force vector and the force vector 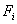 . The second term of equation (6.11) is a contribution from the last element only. This term needs to be treated separately and therefore not included in the expression for . The second term of equation (6.11) is a contribution from the last element only. This term needs to be treated separately and therefore not included in the expression for 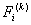 and the present discussion. Using the expressions (6.10) and (6.12), the contribution to equation (6.6) of the and the present discussion. Using the expressions (6.10) and (6.12), the contribution to equation (6.6) of the 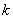 -th element can be written as -th element can be written as
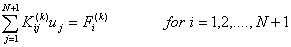 |
(6.13) |
Note that the values of 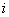 for which for which 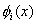 is nonzero over the is nonzero over the 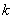 -th element are -th element are 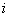 = = 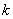 and and 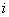 = = 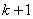 . Therefore, the only nonzero rows of . Therefore, the only nonzero rows of 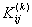 and and 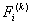 are are 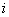 = = 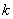 and and 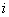 = = 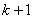 . Thus, the only nonzero equations of the set (6.13) are . Thus, the only nonzero equations of the set (6.13) are 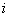 = = 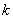 and and 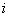 = = 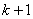 . These equations are as follows: . These equations are as follows:
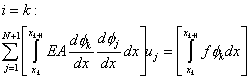 , ,
|
(6.14) |
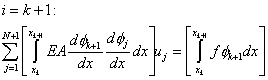 |
(6.15) |
Since, the only values of 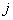 for which for which 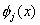 is nonzero over the interval is nonzero over the interval 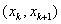 are are 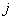 = = 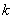 and and 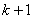 . Therefore, the above equations become: . Therefore, the above equations become:
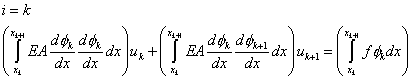 , ,
|
(6.16) |
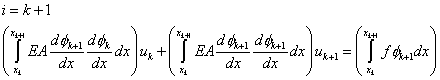 . . |
(6.17) |
In matrix form, this can be written as
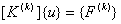 , , |
(6.18) |
where
and
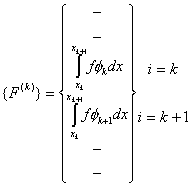 |
(6.20) |
In elemental notation, the above quantities can be written as
and
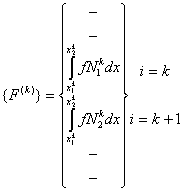 |
(6.22) |
Note that, the elements of 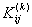 and and 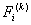 are zero when are zero when  or or 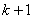 and and 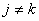 or or 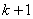 . Thus, . Thus,
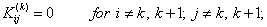 |
(6.23) |
and
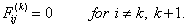 |
(6.24) |
Therefore, these quantities are often expressed as
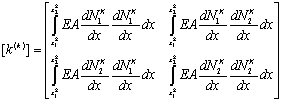 , , |
(6.25) |
and
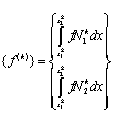 |
(6.26) |
The matrix (6.25) is called as the element stiffness matrix whereas the vector (6.26) is called as the element force vector . Note that the notation for the elemental quantities uses small letters : small k for the stiffness matrix and small f for the force vector. The notation for the corresponding full matrix or full vector uses capital letters : capital K for the stiffness matrix and capital F for the force vector.
The expressions (6.25) and (6.26) help in the systematic evaluation of the global stiffness matrix 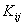 and global force vector and global force vector 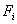 of equation (6.6). The procedure can be described as follows: of equation (6.6). The procedure can be described as follows:
- First, the stiffness matrix and the force vector of each element are evaluated using the expressions (6.25) and (6.26). This can be done using a DO loop. Thus, for
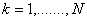 , the elements stiffness matrix , the elements stiffness matrix 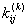 and element force vector and element force vector 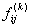 are evaluated using are evaluated using
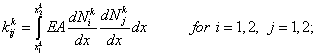 |
(6.27) |
and
 |
(6.28) |
- Next, these quantities are expanded to the full size
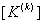 and and 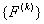 . This is done using the relationship between the local and global node numbering systems. . This is done using the relationship between the local and global node numbering systems.
- Finally, the expanded matrices and vectors of all the elements are added to get the global stiffness matrix
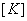 and global force vector and global force vector 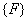 . At this stage, the second term of the expression for . At this stage, the second term of the expression for 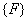 (equation 6.8) also needs to be added. (equation 6.8) also needs to be added.
The last 2 steps constitute what is called as the global assembly procedure. The details of the procedure are discussed in section 6.4. Before that, section 6.3 discusses an example on element calculation.
|