| |
Galerkin Method
We shall use the Galerkin method to obtain an approximate solution. Therefore, the integral form to be used is given by equation (3.68). This equation is rearranged as
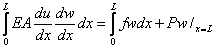 |
(5.4) |
As before, we assume an approximate solution as a series of ( N +1) terms :
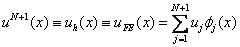 |
(5.5) |
where 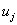 are the unknown coefficients and are the unknown coefficients and 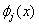 are the basis functions described in the previous section. Note that, now the basis functions are numbered from one rather than from zero (as done in Lecture 4). Therefore the summation index also starts from one, and not from zero. Another departure we make, from the methodology adopted in Lecture 4, is that we do not apply the Dirichlet boundary condition in the beginning. It will be applied later. are the basis functions described in the previous section. Note that, now the basis functions are numbered from one rather than from zero (as done in Lecture 4). Therefore the summation index also starts from one, and not from zero. Another departure we make, from the methodology adopted in Lecture 4, is that we do not apply the Dirichlet boundary condition in the beginning. It will be applied later.
For Galerkin method, we choose the basis functions 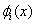 as the weight functions. Thus, as the weight functions. Thus,
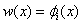 for i=1,2,...,N+1 for i=1,2,...,N+1 |
(5.6) |
Note that these functions are linearly independent and satisfy all the constraints arising out of the three admissibility conditions on 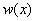 . Substituting the expression (5.6) for . Substituting the expression (5.6) for 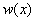 in equation (5.4), we get in equation (5.4), we get
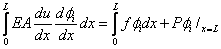 |
for i = 1,2,..., N +1. |
(5.7) |
Now, we write the integral from 0 to L as a sum of the integrals over N elements. Thus, we have
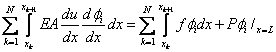 |
for i =1,2,..., N +1. |
(5.8) |
Next, to obtain ( N +1) algebraic equations for the unknowns 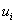 , we substitute the approximation (5.5) for , we substitute the approximation (5.5) for 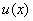 in the above equation. Thus we obtain in the above equation. Thus we obtain
 align="absmiddle"> align="absmiddle"> |
for i = 1,2,..., N +1. |
(5.9) |
Interchanging the sums on the left side, we get
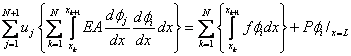 |
for i = 1,2,.., N +1. |
(5.10) |
Now, define the following :
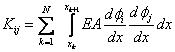 |
for i = 1,2,.., N +1, j = 1,2,.., N +1; |
(5.11) |
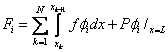 for i = 1,2,...., N +1. for i = 1,2,...., N +1. |
(5.12) |
Then, equation (5.10) becomes :
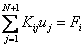 for i = 1,2,.., N +1. for i = 1,2,.., N +1. |
(5.13) |
In matrix form, this can be written as
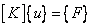 |
(5.14) |
The last term in the expression (5.12) for 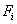 can be simplified as follows. Note that, at the end point x = L , all can be simplified as follows. Note that, at the end point x = L , all 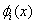 are zero except for i = N +1 (Fig. 5.1). Therefore, the last term is nonzero only for i = N +1. Thus, the expression (5.12) becomes are zero except for i = N +1 (Fig. 5.1). Therefore, the last term is nonzero only for i = N +1. Thus, the expression (5.12) becomes
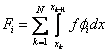 |
for i = 1,2,., N ; |
|
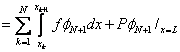 |
for i = N +1. |
(5.15) |
The expressions (5.11) and (5.15) show that the stiffness matrix 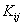 and the force vector and the force vector 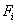 are to be evaluated as the sums of the integrals over N elements. The systematic procedure for this evaluation will be discussed in the next Lecture. However, for given i , the contribution of many elements is zero as shown in the next paragraph. are to be evaluated as the sums of the integrals over N elements. The systematic procedure for this evaluation will be discussed in the next Lecture. However, for given i , the contribution of many elements is zero as shown in the next paragraph.
Consider the expressions (5.11) and (5.15) for 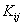 and and 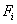 . Note that the functions . Note that the functions 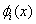 , except for i = 1 and N +1, are zero outside the interval , except for i = 1 and N +1, are zero outside the interval 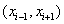 (Fig. 5.1). Therefore, the sums (5.11) and (5.15) for (Fig. 5.1). Therefore, the sums (5.11) and (5.15) for 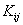 and and 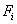 receive the contributions only from the two elements : element i -1 and i, that is, from receive the contributions only from the two elements : element i -1 and i, that is, from 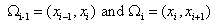 for i = 2,3,.., N . For i = 1, the function for i = 2,3,.., N . For i = 1, the function 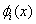 is non zero only for the first element is non zero only for the first element 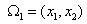 . Thus, for i = 1, . Thus, for i = 1, 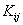 and and 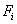 receive the contributions only from the first element. For i = N +1, the function receive the contributions only from the first element. For i = N +1, the function 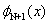 is non-zero only for the last, i.e., Nth element is non-zero only for the last, i.e., Nth element 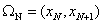 . Thus, for i = N +1, . Thus, for i = N +1, 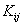 and and 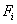 receive the contributions only from the Nth element. Thus , the expressions (5.11) and (5.15) for receive the contributions only from the Nth element. Thus , the expressions (5.11) and (5.15) for 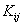 and and 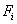 become : become :

|
for i = 1, j = 1,2,.., N +1, (1st element) |
|
(1st element)
|
|
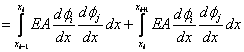 |
for i = 2.., N , j = 1,2,.., N +1, |
|
((i-1)th element) (ith element)
|
|
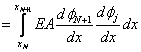 |
for i = N+1, j = 1,2,..,N+1; |
(5.16) |
| (Nth element) |
|
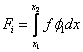 |
for i = 1, |
|
(1st element)
|
|
|
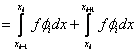 |
for i = 2..,N, |
|
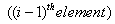 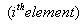
|
|
|
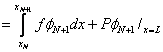 |
for i = N +1. |
(5.17) |
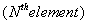 |
|
|
It is observed that the stiffness matrix 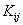 in equation (5.13) is a sparse matrix . More precisely, it is a banded matrix . This can be shown as follows. in equation (5.13) is a sparse matrix . More precisely, it is a banded matrix . This can be shown as follows.
Note that all 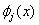 are zero over the next interval are zero over the next interval 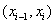 except when j = i -1 and i . Similarly, all except when j = i -1 and i . Similarly, all 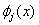 are zero over the next interval are zero over the next interval 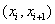 except when j = i and i +1 (Fig. 5.1). Therefore, the only non-zero contributions to the sum on the left side of the equation (5.13) are from j = i -1, i , i +1. Thus, ith equation in the set (5.13) becomes except when j = i and i +1 (Fig. 5.1). Therefore, the only non-zero contributions to the sum on the left side of the equation (5.13) are from j = i -1, i , i +1. Thus, ith equation in the set (5.13) becomes
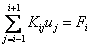 |
(5.18) |
where, for i = 2,3,..., N ,
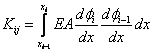
|
for j = 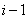 , , |
|
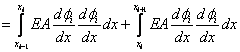 |
for j = i, |
|
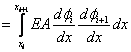 |
for j = i +1, |
|
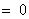 |
for remaining j |
(5.19) |
Further, for i = 1, the only non-zero contributions to the sum on the left side of equation (5.13) come from j =1 and 2. Thus
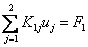 |
(5.20) |
where
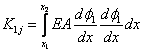 |
for j = 1, |
|
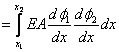 |
for j = 2, |
|
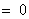 |
for remaining j . |
(5.21) |
Similarly, for i = N +1, the only non-zero contributions to the sum on the left side of equation (5.13) come from j = N and N +1. Thus,
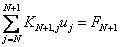 |
(5.22) |
where
Thus, ith equation has non-zero elements only in the columns j = i-1, i , and i +1. The remaining columns are zero. Further, the 1st equation has non-zero elements only in the 1st and 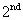 columns . Similarly, the last equation (i.e., columns . Similarly, the last equation (i.e., 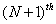 equation) has non-zero elements only in the equation) has non-zero elements only in the 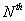 and and 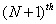 columns. Thus, the matrix columns. Thus, the matrix 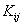 is a banded matrix. is a banded matrix.
|