| |
Mesh and Global Basis Functions
As mentioned in section 4.1, the piecewise linear basis functions are generated by dividing the domain  into many parts (Fig. 5.1). Since this is a one-dimensional problem, the domain into many parts (Fig. 5.1). Since this is a one-dimensional problem, the domain  is identical to an interval of length L. is identical to an interval of length L.
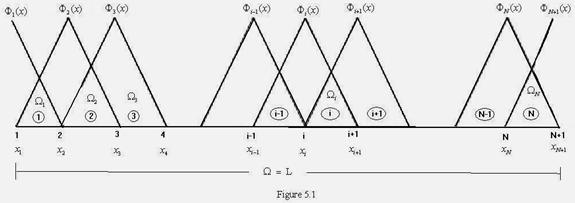
Figure 5.1
To generate (N +1) basis functions, we divide the domain into N parts using the (N -1) intermediate points and the two end points. These points are called as nodes . Thus, we have ( N +1) nodes. We number these nodes sequentially as shown in Fig. 5.1. In Fig. 4.3 we had denoted the coordinate of the first node as 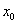 . But, now we label it as . But, now we label it as 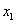 . Thus, the coordinate of the ith node is denoted by . Thus, the coordinate of the ith node is denoted by 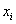 . We place the nodes at the points of . We place the nodes at the points of
- discontinuities in the geometry,
- discontinuities in the material properties, and
- discontinuities in the loading (which also includes the points of application of the concentrated forces)
Otherwise the nodes are equally spread.
The parts in which the domain is divided by nodes are called as the elements . These elements are also numbered sequentially as shown in Fig.5.1. Thus, ith element, denoted by 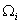 , is defined by , is defined by
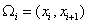 for i = 1,2,..., N for i = 1,2,..., N |
(5.1) |
If the nodes are equally spaced, then the length of each element is equal. Let this length be denoted by h . Then
h = 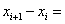 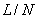 for i = 1,2,., N . for i = 1,2,., N . |
(5.2) |
The division of the domain into the elements and the nodes is called as the mesh . When all the elements are of the same size, it is called as the uniform mesh. The quantity h is called as the (uniform) mesh size .
The piecewise linear basis functions are defined as follows. The functions 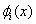 (except (except 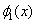 and and 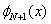 ) are zero outside the interval ) are zero outside the interval 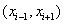 . Within the interval, they are piecewise linear with the maximum value of unity at . Within the interval, they are piecewise linear with the maximum value of unity at 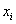 . Thus, . Thus, 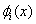 can be expressed as : can be expressed as :
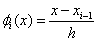 |
for 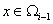 , , |
|
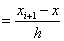 |
for 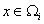 , , |
|
| = 0 |
for 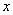 belonging to other elements, belonging to other elements, |
|
| |
for i = 1,2,.., N . |
(5.3) |
Note that the function 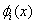 has only a local support over the interval has only a local support over the interval 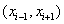 . .
|