Galerkin Method
In Galerkin method, we choose
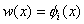 |
for 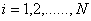 . . |
(3.76) |
Note that the constraints on 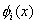 arising out of the admissibility conditions of arising out of the admissibility conditions of 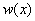 are as follows. The first admissibility condition requires that the functions are as follows. The first admissibility condition requires that the functions 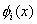 must be zero at must be zero at 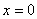 , (that is, at the point of application of the Dirichlet boundary condition on , (that is, at the point of application of the Dirichlet boundary condition on 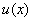 ). Note that this constraint is identical to the condition (3.71). The second condition implies that ). Note that this constraint is identical to the condition (3.71). The second condition implies that 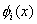 should be unconstrained at should be unconstrained at 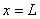 . The third condition requires that the derivative . The third condition requires that the derivative 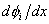 must be finite over the whole interval (0, L ). must be finite over the whole interval (0, L ).
Substituting the expression (3.76) for 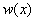 in equation (3.74), we get in equation (3.74), we get
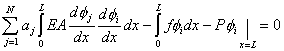 |
for 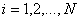 |
(3.77) |
Now, define the following :
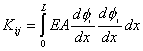 , , |
(3.78) |
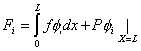 |
(3.79) |
Then, equation (3.77) becomes
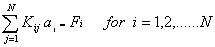 |
(3.80) |
In matrix form, this can be written as :
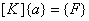 |
(3.81) |
Note that, we get the same set of algebraic equations as in the Ritz method (equations 3.13-3.16). Therefore, as in the Ritz method, the stiffness matrix 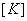 is symmetric and positive definite. is symmetric and positive definite.
|