Higher Order Lagrangian Approximations

In constructing higher order approximations, we use the property of spatial invariance or geometric isotropy . This property states that the form of the approximating function must be independent of the orientation of the coordinate system. The complete polynomials possess this property. This is because a complete polynomial in ( x, y ) coordinate system transforms into another complete polynomial of the same degree (with different coefficients) into a rotated coordinate system .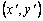

The monomials of degree n for various values of n have been arranged as shown in Fig. 22.1. This figure is called as Pascal Triangle . The complete polynomial of degree p contains all the monomials upto degree p , i.e., all the monomials of the degree 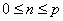. Thus, the number of monomials in a complete polynomial of degree p is given by

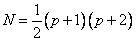(23.1)

Thus, in a complete polynomial of degree p = 1, there are N = 3 monomials, namely 1, x and y. Similarly, in a complete polynomial of degree p = 2, there are N = 6 monomials, namely 1, x, y , x² , xy and y² . Note that, the number of coefficients in a complete polynomial of degree p is also equal to N .

Axis of symmetry

Figure 23.1 Pascal Triangle or Monomials of Degree n Arranged in the Order of Increasing n .

If a complete polynomial of degree p is to be used as an approximation, the number of coefficients N in the polynomial must be equal to the degrees of freedom per element. Since, this is a Lagrangian element, the degree of freedom per node is one. Thus, the degrees of freedom per element are exactly equal to the number of nodes per element. Therefore, the number of nodes per element must be equal to N , i.e. the number of coefficients in the polynomial.

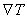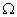Note that, for the weighted residual integral (eq. 20.13) to be finite, the approximation for the primary variable T must be such that is piecewise continuous over the domain with only finite discontinuities. Therefore, the approximation must be such that the primary variable is continuous across the interelement boundaries. We are using a complete polynomial of degree p as the approximation over a typical element. If the coordinate along a boundary segment is denoted by s , then the variation of the primary variable along the boundary segment becomes a 1-D polynomial in s of degree p . To make the primary variable continuous across the interelement boundaries, its variation along the common boundary segment must be the same as that of the adjoining element. For this to happen, the number of nodes (which is equal to the degrees of freedom) on the common boundary segment must be equal to ( p + 1). Since the triangular element has three boundary segments, the number of boundary nodes becomes :

Since 3 nodes are common to 3 pairs of the boundaries, they must be subtracted from 3( p + 1) to get the number of boundary nodes N_b .

The remaining nodes must be in the interior of the element. Thus, the number of internal nodes is given by

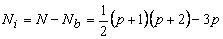(23.3)

Thus, when a complete polynomial of degree p = 1 is used, as per equations (23.1) - (23.3), the number of various nodes is N = N_b = 3 and N i = 0. Similarly, when p = 2 is used, the number of various nodes is N = N_b = 6 and N_i = 0. But for the case of p = 3, the number of various nodes is N = 10, N_b = 9 and N_i = 0. Thus, there is one internal node.