| |
Expressions for the Element Stiffness Matrix and Element Force Vector
As stated earlier, we use the weighed residual formulation to derive the finite element equations. The corresponding integral form is gives by eq. (20.13). Further, we have decided to use the Galerkin scheme. Then, the weight functions are identical to the global basis functions :
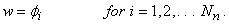 |
(21.20) |
First, we substitute the above expression for the weight function in the integral from (eq. 20.13). Thus, we obtain
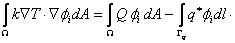 |
(21.21) |
Next, we write the integral over  as a sum of the integrals over as a sum of the integrals over  elements. Thus, we get elements. Thus, we get
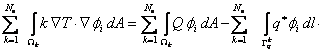 |
(21.22) |
Here, 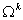 is the domain of element k and is the domain of element k and  is the intersection of the element k with the boundary is the intersection of the element k with the boundary 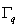 . Note that, for many elements . Note that, for many elements  is zero. For the mesh of Fig. 21.1, is zero. For the mesh of Fig. 21.1,  is zero for all k except for k = 1, 2 and 5. Now, we substitute the finite element approximation (eq. 21.14) in terms of the global basis functions in the above equation. We obtain is zero for all k except for k = 1, 2 and 5. Now, we substitute the finite element approximation (eq. 21.14) in terms of the global basis functions in the above equation. We obtain
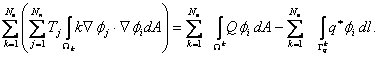 |
(21.23) |
Now, we interchange the sums on the left hand side to get
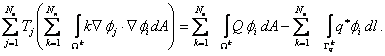 |
(21.24) |
Finally, we define the following quantities :
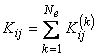 |
i , j = 1, 2, . . . . , Nn . |
(21.25) |
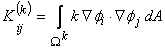 |
i , j = 1, 2, . . . . , Nn |
(21.26) |
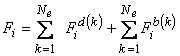 |
i = 1, 2, . . . . , Nn |
(21.27) |
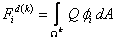 |
i = 1, 2, . . . . , Nn |
(21.28) |
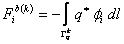 |
i = 1, 2, . . . . , Nn |
(21.29) |
Then, eq. (21.24) becomes :
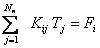 |
i = 1, 2, . . . . , Nn |
(21.30) |
These are the finite element equations. In matrix form, they can be written as :
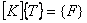 |
(21.31) |
where [ K ] is called as the global coefficient matrix , 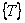 is called as the global right side vector and is called as the global right side vector and 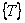 is called as the vector of global dof. For the heat condition problem, is called as the vector of global dof. For the heat condition problem, 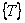 is called as the global temperature vector , [K] is called as the global conductivity matrix and {F} is called as the global heat flux vector . is called as the global temperature vector , [K] is called as the global conductivity matrix and {F} is called as the global heat flux vector .
Equations (21.25) and (21.27) show that the global coefficient matrix and global right side vector consists of the contributions 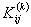 , , 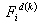 and and 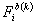 from the elements from the elements 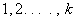 . The expressions for . The expressions for 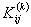 , , 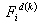 and and 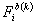 for the k -th element can be simplified as follows. Note that the values of i and j for which for the k -th element can be simplified as follows. Note that the values of i and j for which 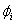 and and 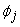 are nonzero over the element are given by eq. (21.17) : are nonzero over the element are given by eq. (21.17) :
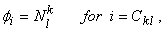 |
|
| = 0 for other I , |
|
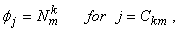 |
|
| = 0 for other j . |
(21.32) |
Thus, only the following 9 elements of 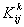 are nonzero : are nonzero :
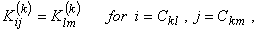 |
|
| = 0 for other i and j |
(21.33) |
where
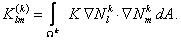 |
(21.34) |
Similarly, only the following 3 elements of 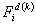 and and 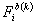 are nonzero : are nonzero :
 |
|
| = 0 for other i |
(21.35) |
where
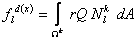 |
(21.36) |
and
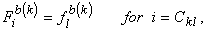 |
|
| = 0 for other i |
(21.37) |
where
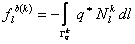 |
(21.38) |
It is convenient to express eqs. (21.34), (21.36) and (21.3) in an array form. For this purpose, define the following arrays :
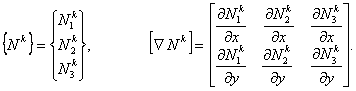 |
(21.39) |
Then, eqs. (21.34), (21.36) and (21.38) become :
The 3×3 matrix 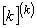 is called as the element coefficient matrix . The 3×1 ectors is called as the element coefficient matrix . The 3×1 ectors 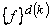 and and 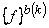 are called as the element right side vectors . The superscript 'd' on are called as the element right side vectors . The superscript 'd' on 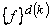 indicates that it is a contribution from the domain of element k while the superscript 'b' on indicates that it is a contribution from the domain of element k while the superscript 'b' on 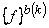 denotes that it is a contribution from the boundary of the element k ( if it lies on denotes that it is a contribution from the boundary of the element k ( if it lies on 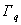 ). Note that, for many elements, ). Note that, for many elements, 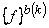 would be zero since none of their boundaries would lie on would be zero since none of their boundaries would lie on 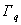 . For the mesh of Fig. 21.1, . For the mesh of Fig. 21.1, 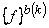 would be a zero vector for all the elements except for the element no. 1, 2 and 5. would be a zero vector for all the elements except for the element no. 1, 2 and 5.
|