Simplest Approximation
Figure 21.1 shows a 2-D domain divided into a uniform mesh of 3-noded triangular elements. It also shows an element numbering system, a global node numbering system and global dof. The element numbers are encircled. The total number of elements is denoted by N e and the total number of nodes by N n .
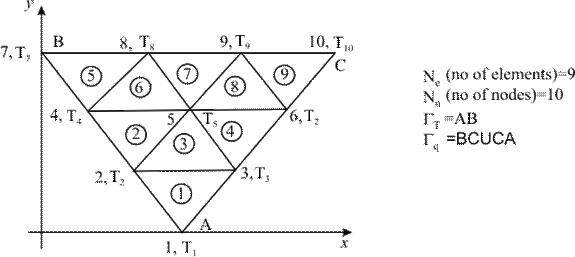
Figure 21.1 Uniform Mesh of 3-Noded Triangular Elements
Figure 21.2 shows a typical element k . It also shows the local node numbering system, and the nodal coordinates 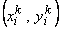 and nodal degrees of freedom (dof) and nodal degrees of freedom (dof) 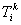 of local node i . The local node numbering can start from any vertex but it must be counter clock wise. The notation for the coordinates and dof has the superscript k indicating that these quantities belong to the element k . This is called as local notation. of local node i . The local node numbering can start from any vertex but it must be counter clock wise. The notation for the coordinates and dof has the superscript k indicating that these quantities belong to the element k . This is called as local notation.
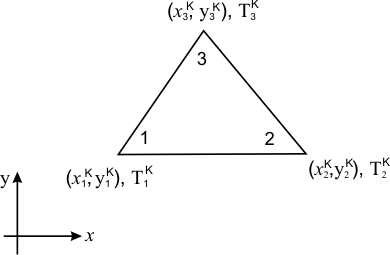
Figure 21.2 Typical 3-Noded Triangular Element k
Each node has a one dof. Thus, there are totally 3 dof per element. Therefore, we need 3 linearly independent basis functions. We choose the lowest three monomial functions as the basis functions. Then, the finite element approximation for k -th element becomes :
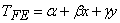 |
(21.1) |
where 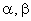 and and 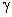 are unknown coefficients. This is a complete linear polynomial in x and y . To express these unknown coefficients in terms of the elemental dof, we evaluate T at the 3 nodes, i.e., at are unknown coefficients. This is a complete linear polynomial in x and y . To express these unknown coefficients in terms of the elemental dof, we evaluate T at the 3 nodes, i.e., at 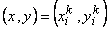 . Thus, we get . Thus, we get
Solving these 3 equations, we get
where
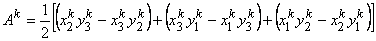 |
(21.4) |
is the area of the element. If the local numbering is done clockwise, then  becomes negative. Substituting the expressions for becomes negative. Substituting the expressions for  and and  in eq. (21.1) and rearranging the terms, we get in eq. (21.1) and rearranging the terms, we get
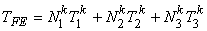 |
(21.5) |
where the shape functions 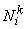 are given by are given by
Note that, like the expression (21.1), each shape function is also a complete linear polynomial in x and y. It is easy to verity that these shape functions satisfy the property :
 |
(21.7) |
Thus, the shape function 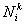 has the value 1 at the node i and zero at the other two nodes. Figure 21.3 shows the variation of has the value 1 at the node i and zero at the other two nodes. Figure 21.3 shows the variation of 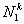 over the element k . Variations of the other two shape functions will be similar. over the element k . Variations of the other two shape functions will be similar.
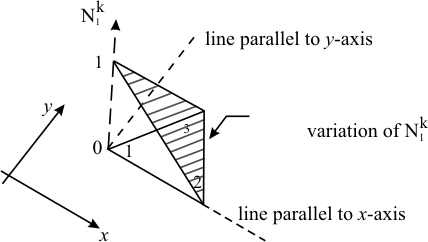
Figure 21.3 Variation of 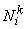 over the Element k over the Element k
These are called as linear Lagrangian shape functions and the corresponding triangular element is called as the first order Lagrangian triangular element .
To facilitate numerical integration of the coefficient matrix, we need to transform each (triangular) element to a master (triangular) element for which the expression for numerical integration is available. The master element is an isosceles right-angled triangle with equal sides being unity. This element is shown in Fig. 21.4. The coordinates  are called as natural coordinates . are called as natural coordinates .
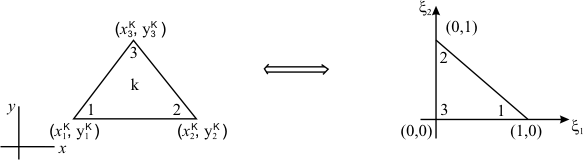
Figure 21.4 Mapping of a Triangular Element onto the Master Element
Since straight boundaries of a triangular element get mapped onto the straight boundaries of the master element, the mapping can be expressed as a linear relation between ( x , y ) and 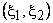 coordinates : coordinates :
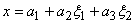 |
|
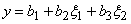 |
(21.8) |
Here, the unknown coefficients 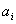 and and 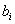 are determined from the conditions that the nodes 1, 2, 3 of the triangular element map respectively onto the vertices (1, 0), (0, 1) and (0, 0) of the master element. Thus, we get are determined from the conditions that the nodes 1, 2, 3 of the triangular element map respectively onto the vertices (1, 0), (0, 1) and (0, 0) of the master element. Thus, we get
Solving these 6 equations for 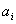 and and 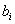 and substituting these expressions into eq. (21.8), the mapping function becomes: and substituting these expressions into eq. (21.8), the mapping function becomes:
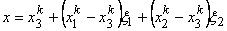 |
|
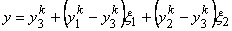 |
(21.10) |
The shape function expressions in natural coordinates
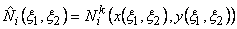 |
(21.11) |
are obtained by substituting the mapping function (21.10) into eq. (21.6). We get
Note that, using the above expressions of the shape functions, the mapping function for element k (eq. 21.10) becomes :
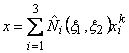 |
|
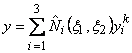 |
(21.13) |
When we use the linear Lagrangian shape functions. The approximation in terms of the global basis functions for the mesh shown in Fig. 21.1 becomes :
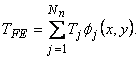 |
(21.14) |
Here, 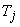 are the global degrees of freedom (i.e., values of the temperature at global nodes) and are the global degrees of freedom (i.e., values of the temperature at global nodes) and 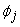 are the global basis functions. Over a typical element k , all but three global basis functions reduce to zero and the three non-zero global basis functions reduce to the linear Lagrangian shape function are the global basis functions. Over a typical element k , all but three global basis functions reduce to zero and the three non-zero global basis functions reduce to the linear Lagrangian shape function 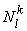 . .
To obtain the relationship between 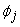 and and 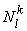 , we use the connectivity matrix [ C ]. This matrix, which relates the local and global node numbering systems, is defined by the relation (eq. 6.35) : , we use the connectivity matrix [ C ]. This matrix, which relates the local and global node numbering systems, is defined by the relation (eq. 6.35) :
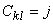 |
(21.15) |
In the above equation, the row index k denotes the element number, the column index l denotes the local node number and the value j is the global node number of the local node l belonging to the element k . Using the above definition, the connectivity matrix corresponding to the mesh of Fig. 21.1 can be expressed as :
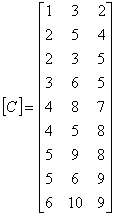 |
(21.16) |
Using the definition of [ C ] (eq. 21.15), the relationship between the global basis functions 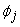 and the elemental shape functions and the elemental shape functions 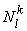 of the element k can be expressed as : of the element k can be expressed as :
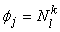 , , 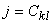 |
|
| = 0 for other j . |
(21.17) |
As an example, consider 3rd element (i.e., k = 3). From the 3 rd row of [ C ] (eq. 21.16), we get the following values of the global nodes numbers corresponding to three local nodes of the 3rd element :
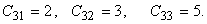 |
(21.18) |
Then, for the 3 rd element (i.e., k = 3) eq. (21.17) gives the following relationship between 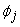 and and 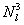 : :
|