C1- Continuity
The integral form of the weighted residual formulation (eq. 18.8) contains the second derivatives of the primary variable 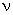 and the weight function w . As stated earlier, for this integral to be finite, and the weight function w . As stated earlier, for this integral to be finite, 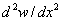 must be piecewise continuous on the internal (0, L ) with only finite discontinuities. Additionally, must be piecewise continuous on the internal (0, L ) with only finite discontinuities. Additionally, 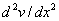 also must be piecewise continuous on the internal (0, L ) with only finite discontinuities. This is shown in Fig. 18.2. also must be piecewise continuous on the internal (0, L ) with only finite discontinuities. This is shown in Fig. 18.2.
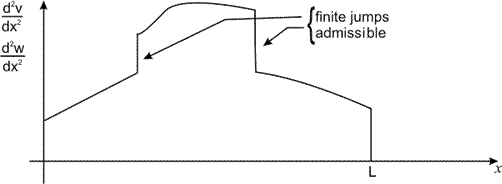
Figure 18.2 Permissible Discontinuities in Second Derivatives of the Primary Variable and Weight Function
These requirements mean 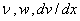 and and 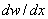 should be continuous over the internal (0, L ). As stated in the introduction, the approximations (for the primary variable) in which both the primary variable as well as its first derivative are continuous are called as the should be continuous over the internal (0, L ). As stated in the introduction, the approximations (for the primary variable) in which both the primary variable as well as its first derivative are continuous are called as the 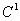 - Continuity Approximations . Thus, for the beam problem, we need to choose the degrees of freedom and shape functions which will ensure the - Continuity Approximations . Thus, for the beam problem, we need to choose the degrees of freedom and shape functions which will ensure the 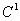 - continuity of the approximation. Such shape functions are developed in the next Lecture. - continuity of the approximation. Such shape functions are developed in the next Lecture.
The integral form of the variational formulation (eq. 18.11) also contains the second derivative of the primary variable 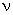 . Therefore, the continuity requirement for this formulation is also the same, namely the . Therefore, the continuity requirement for this formulation is also the same, namely the 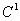 -continuity of the approximation. -continuity of the approximation.
|