| |
Virtual Work and Variational Formulations
We can similarly obtain the other integral forms. Let 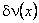 be the virtual (transverse) displacement at cross-section x . Further, let be the virtual (transverse) displacement at cross-section x . Further, let 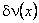 belong to the same class of admissible functions from which w ( x ) is chosen. Then setting w equal to belong to the same class of admissible functions from which w ( x ) is chosen. Then setting w equal to 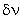 in eq. (18.8), we get in eq. (18.8), we get
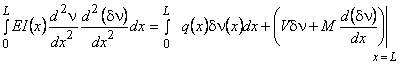 |
(18.9) |
Now, we treat the symbol 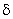 in the expression in the expression 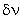 as the operator called as the variational operator . The quantity as the operator called as the variational operator . The quantity 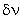 is called as the variation of is called as the variation of 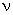 . Using the properties of . Using the properties of 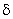 - operator from section 5 of Lecture 2, we can convert eq. (18.9) to the following form : - operator from section 5 of Lecture 2, we can convert eq. (18.9) to the following form :
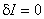 |
(18.10) |
where
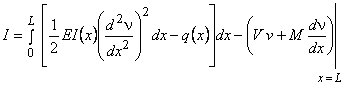 |
(18.11) |
The functional I is called as the Variational Functional of the boundary value problem (18.1(a), 18.1(b), 18.1(c)). This is the integral form to be used for the Variational Formulation . This integral needs to be extremized to obtain the solution of the boundary value problem.
The extremizing function 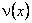 needs to satisfy the following three conditions, which are similar to the conditions on the weight function w ( x ) : needs to satisfy the following three conditions, which are similar to the conditions on the weight function w ( x ) :
- The function
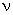 must satisfy the kinematic boundary conditions 18.1(b). Thus must satisfy the kinematic boundary conditions 18.1(b). Thus 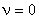 and and 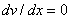 at x = 0. Further, at this point, the variation at x = 0. Further, at this point, the variation 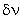 must satisfy the conditions must satisfy the conditions 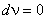 and and 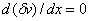 at x = 0. at x = 0.
- The function
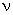 , its variation , its variation 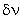 and the first derivatives of and the first derivatives of 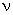 and and 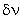 must be unconstrained where the force boundary conditions (eq. 18.1(c)) are specified. Thus, must be unconstrained where the force boundary conditions (eq. 18.1(c)) are specified. Thus, 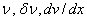 and and 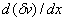 must be unconstrained at x = L . must be unconstrained at x = L .
- The function
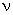 must be smooth enough to make the functional I finite. Thus, must be smooth enough to make the functional I finite. Thus, 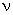 be must be such that be must be such that 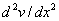 is finite at every point of the internal (0, L ). is finite at every point of the internal (0, L ).
The equation 18.1 (a) is called as the Euler Equation of the functional I (eq. 18.11). Further, the boundary conditions 18.1(b) are called as the Essential Boundary Conditions , and the conditions 18.1(c) are called as the Natural Boundary Conditions.
Physically, the quantity I (eq. 18.11) is the total potential energy of the beam. Therefore, the variational formulation states the following principle. The solution of the boundary value problem (18.1(a), 18.1(b), 18.1(c)) extremizes the total potential energy of the beam. This is called as the Principle of the Stationary Value of the Total Potential Energy . In eq. (18.9), the left hand side represents the virtual work of the internal forces while the right hand side represents the virtual work of the external forces q ( x ) and V and the moment M . Thus, equation (18.9) states the following. For 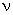 to be a solution of the boundary value problem (18.1(a), 18.1(b), 18.1(c)), the virtual work of the external forces must be equal to the virtual work of the internal forces. to be a solution of the boundary value problem (18.1(a), 18.1(b), 18.1(c)), the virtual work of the external forces must be equal to the virtual work of the internal forces.
|