| |
Algorithm for Subroutine MAKE - MESH
If 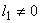 , the uniform mesh for the part one is shown in Fig. 15.1 for the case of 2-noded element. , the uniform mesh for the part one is shown in Fig. 15.1 for the case of 2-noded element.
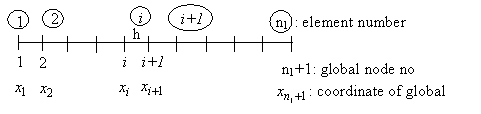
Since the length is l1 and the number of elements is 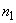 , the uniform mesh size for the part one is : , the uniform mesh size for the part one is :
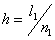 . . |
(15.5) |
If 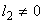 , the uniform mesh for the part two would be similar to the mesh of Fig. 15.1, except that now the element number would start from , the uniform mesh for the part two would be similar to the mesh of Fig. 15.1, except that now the element number would start from 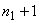 and the global node number would start from and the global node number would start from 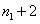 (if (if 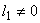 ). If ). If 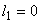 , both would start from one each. Further, the uniform Mesh size for the part two would be : , both would start from one each. Further, the uniform Mesh size for the part two would be :
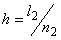 |
(15.6) |
If 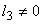 , the uniform mesh for the part three would be similar to the mesh of Fig. 15.1 except for the starting element number and starting global node number. The element number would start from: (i) , the uniform mesh for the part three would be similar to the mesh of Fig. 15.1 except for the starting element number and starting global node number. The element number would start from: (i) 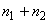 if if 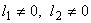 or (ii) or (ii) 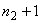 if if 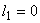 or (iii) or (iii) 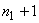 if if 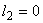 . Similarly, the global node number would start from : (i) . Similarly, the global node number would start from : (i) 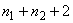 if if 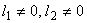 or (ii) or (ii) 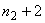 if if 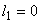 or (iii) or (iii) 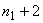 if if 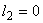 . Further, the uniform mesh size for the part three would be : . Further, the uniform mesh size for the part three would be :
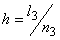 |
(15.7) |
We define the following notation :
ept : element number at the end of which point force is applied (integer),
nnode : number of global nodes (integer),
nelem : number of elements (integer),
x (i) : coordinate vector (real),
C(i,j) : connectivity matrix (real),
matid(i) : material code vector (integer).
Now, the algorithm for the subroutine MAKE - MESH can be written as follows.
- Initialize : nnode = 1, nelem = 0, x(1) =
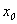
- If
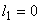 , go to the next step , go to the next step
If 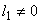 , , 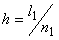
do 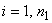
nnode = nnode + 1
nelem = nelem + 1
x (nnode) = x (nnode-1) + h
C (nelem, 1) = nnode - 1
C ( nelem, 2) = nnode
matid (nelem) = matdom _1
enddo
If 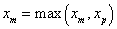 , ept = nelem , ept = nelem
- If
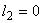 , go to the next step , go to the next step
If 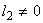 , , 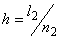
repeat the do loop of (ii)
If 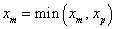 , ept = nelem , ept = nelem
- If
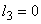 , stop , stop
If 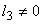 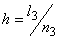
repeat the do loop of (ii)
Note that this algorithm needs to be appropriately modified when the number of nodes per element is more than two.
|