| |
Algorithm for Subroutine READ - INPUT
A typical algorithm for reading the input data can be as follows:
- Domain Data
- read the coordinates
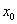 and and 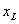 of the left and right ends. of the left and right ends.
- determine L :
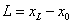 . .
- Geometric Data
- read the geometric transition point
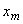 . .
- read the areas of cross-section at
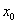 , , 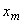 and and 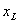 : : 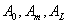 . .
- calculate the coefficients
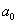 and and 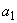 in the linear expression for the area for the two parts using equations (14.2) and (14.3). in the linear expression for the area for the two parts using equations (14.2) and (14.3).
- Material Data
Note that the material transition point is the same as the geometric transition point ( 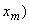 . .
- read the constant Young's moduli E1 and E2 of two parts.
- Force Data
- read the coefficients f0 , f1 and f2 in the quadratic variation of f .
- read the location ( x p ) and the value ( P 1 ) of the point force.
- Boundary Data
First we define the code for the boundary conditions.
For the Dirichlet boundary condition, code = 1,
For the Neumann boundary condition, code = 2,
For the spring boundary condition, code = 3.
Now, the algorithm for the boundary data is as follows :
- read the code for the boundary condition at
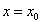 . .
If code = 1, read the specified displacement 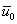 , ,
If code = 2, read the specified force Q,
If code = 3, read the spring constant 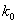 and the initial spring deflection and the initial spring deflection 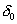 . .
- read the code for the boundary condition at
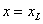 . .
If code = 1, read the specified displacement 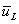 , ,
If code = 2, read the specified force P ,
If code = 3, read the spring constant 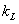 and the initial spring deflection and the initial spring deflection 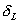 . .
Note :
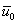 and and 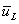 are considered positive if they are along positive x - direction. are considered positive if they are along positive x - direction.- Q and P are considered positive if they are tensile.
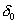 and and 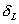 are considered positive if they are compressive. are considered positive if they are compressive.
- Mesh Data
First we define the lengths l1 , l 2 and l 3 of the three parts as follows :
where
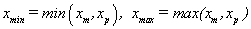 |
(15.2) |
There are special cases in which either l1 or l2 or l3 or any two of them are zero. These cases as follows:
If 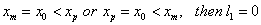 If If 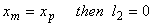
If 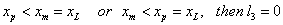 If If 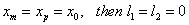
If 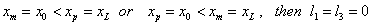
If 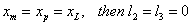
Note that if 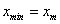 , then the Young's modulus of part 1 is E1 and that of parts 2 and 3 is E2 . On the other hand, if , then the Young's modulus of part 1 is E1 and that of parts 2 and 3 is E2 . On the other hand, if 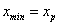 , then the Young's modulus of parts 1 and 2 is E1 and that of part 3 is E2 . To take care of this situation, we introduce a material code for all the three parts. These codes are matdom _1, matdom _2 and matdom _3. Then, the Young's moduli corresponding to these material codes are as follows. , then the Young's modulus of parts 1 and 2 is E1 and that of part 3 is E2 . To take care of this situation, we introduce a material code for all the three parts. These codes are matdom _1, matdom _2 and matdom _3. Then, the Young's moduli corresponding to these material codes are as follows.
| E = E1 for matdom _1, E = E2 for matdom _3; |
(15.3) |
E = E1 for matdom _2 for 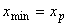 , , |
|
= E2 for matdom _2 for 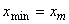
|
(15.4) |
We assume that the mesh is uniform over all the three parts. Let n1 , n2 , n3 be the number of elements in each part. Now, the algorithm for mesh data is as follows.
- calculate xmin and xmax using eq. (15.2).
- calculate l1 , l2 and l3 using eq. (15.1).
- Assign the Young's modulus for the material code using eq.(15.3)-(15.4).
- read the number of elements (n1 , n2 , n3 ) for each part
- read the order of approximation p.
|