Numerical Integration Expressions for 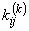 and and 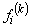
Now, we apply the Gauss quadrature rule (equation 12.1) to the expressions (11.48) and (11.51) for the element coefficient matrix 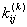 and the element force vector and the element force vector 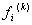 . To select the number of Gauss point, we used to evaluate the degree of the integrands. For this purpose, we rewrite these expressions as: . To select the number of Gauss point, we used to evaluate the degree of the integrands. For this purpose, we rewrite these expressions as:
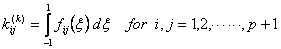 , , |
(12.30) |
and
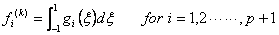 , , |
(12.31) |
where the integrands are given by
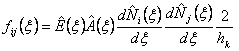 , , |
(12.32) |
and
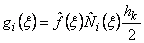 . . |
(12.33) |
For the sake of concreteness, we make the following choices:
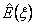 is a constant function of x (constant Young's modulus) is a constant function of x (constant Young's modulus)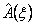 is a linear function of x (tapered bar) is a linear function of x (tapered bar) 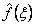 is a quadratic function of x (quadratic loading) is a quadratic function of x (quadratic loading)- The order of approximation is p . Thus, degree of
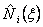 is p and that of its derivative is is p and that of its derivative is 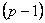
Now, the degree of the integrand 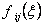 becomes becomes
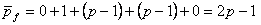 , , |
(12.34) |
and that of 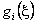 is given by is given by
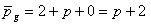 . . |
(12.35) |
Let the maximum of 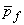 and and 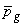 be be 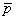 . Thus, . Thus,
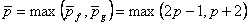 . . |
(12.36) |
Now, we use equation (12.29) to select the number of Gauss points. Using equations (12.34) and (12.36), we get the following values of n for 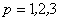
Similarly, we can obtain n for 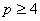 . .
Application of the Gauss quadrature rule (equation 12.1) to the integrals (12.30) - (12.31) leads to the following expressions for 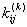 and and 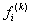 : :
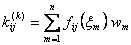 , , |
(12.38) |
and
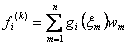 |
(12.39) |
where 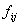 and and 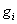 are given by equations (12.32)-(12.33) and n is given by equation (12.37). The Gauss point coordinates are given by equations (12.32)-(12.33) and n is given by equation (12.37). The Gauss point coordinates 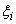 and the weights and the weights 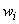 corresponding to n are to be taken from Table 12.1. corresponding to n are to be taken from Table 12.1.
|