Gauss Quadrature Rule
Consider a function 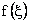 defined over the master element. Note that, as stated in the last lecture, defined over the master element. Note that, as stated in the last lecture, 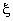 is called as the natural coordinate and varies from -1 to 1. In any numerical integration scheme, the integral is expressed as a sum over certain points of the domain of integration called as sampling points . A typical term in the sum consists of the value of the function at that point multiplied by a suitable number called as the weight . Thus, is called as the natural coordinate and varies from -1 to 1. In any numerical integration scheme, the integral is expressed as a sum over certain points of the domain of integration called as sampling points . A typical term in the sum consists of the value of the function at that point multiplied by a suitable number called as the weight . Thus,
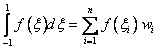 |
(12.1) |
Here, 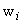 are the weights. In case of Gauss quadrature rule, the sampling points are the weights. In case of Gauss quadrature rule, the sampling points 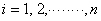 are called as the Gauss points and are called as the Gauss points and 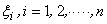 are called as Gauss points coordinates. They are shown in Fig. 12.1, In case of Gauss quadrature rule, the Gauss points are symmetrically located about the origin are called as Gauss points coordinates. They are shown in Fig. 12.1, In case of Gauss quadrature rule, the Gauss points are symmetrically located about the origin 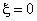 (see Fig. 12.1). Further, the weights corresponding to a pair of symmetrically located Gauss points are the same. (see Fig. 12.1). Further, the weights corresponding to a pair of symmetrically located Gauss points are the same.
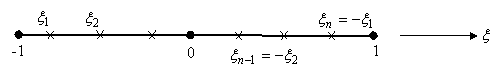
Figure 12.1 Gauss points used in Gauss quadrature rule
In some numerical integration schemes like the Newton-Cotes formulas, the sampling points are chosen a priori .Then the weights are determined by approximating the function by a polynomial of degree 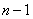 where where 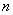 is the number of sampling points. In Gauss quadrature rule, the sampling points (called as the Gauss points) are chosen so as to minimize the error between the exact and approximate values. Therefore, the Gauss point coordinates become the roots of the Legendre polynomials . As a result, this numerical integration scheme is also called as the Gauss-Legendre quadrature rule. is the number of sampling points. In Gauss quadrature rule, the sampling points (called as the Gauss points) are chosen so as to minimize the error between the exact and approximate values. Therefore, the Gauss point coordinates become the roots of the Legendre polynomials . As a result, this numerical integration scheme is also called as the Gauss-Legendre quadrature rule.
In this lecture, we do not present the exact derivation of the Gauss point coordinates and the corresponding weights. Instead, we provide a simpler derivation. In this derivation, we use the following observation. If 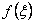 is a polynomial in is a polynomial in 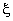 , then there exists a degree , then there exists a degree 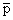 of of 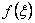 for which the Gauss quadrature rule is exact. We find the values of the Gauss point coordinates and weights and the corresponding value of for which the Gauss quadrature rule is exact. We find the values of the Gauss point coordinates and weights and the corresponding value of 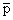 by trial and error method. In this method, we try the Gauss quadrature rule successively for by trial and error method. In this method, we try the Gauss quadrature rule successively for 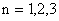 using the polynomials of various degrees starting from one. using the polynomials of various degrees starting from one.
- One point rule (
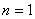 ) )
Since the Gauss points are symmetrically located, for a one point rule, the Gauss point has to be at the centre. Thus,
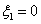 |
(12.2) |
The one point Gauss quadrature rule is
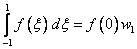 |
(12.3) |
We find 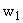 by assuming that one point rule is exact for the polynomial of degree 0: by assuming that one point rule is exact for the polynomial of degree 0:
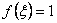 |
(12.4) |
Substituting the above expression for 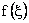 in equation (12.3), we get in equation (12.3), we get
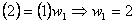 |
(12.5) |
Thus, the one point Gauss quadrature rule becomes:
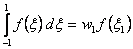 , , |
(12.6a) |
where
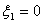 , , |
(12.6b) |
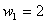 |
(12.6c) |
Next, we try the one point rule for a polynomial of degree 1:
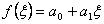 |
(12.7) |
We find that the above rule gives
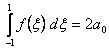 , , |
(12.8) |
that is the exact value. However, when we apply the one point rule to the polynomial of degree 2:
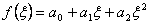 , , |
(12.9) |
we get
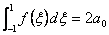 , , |
(12.10) |
which is different from the exact value 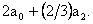 Thus, Thus,  for for 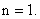 Next, we consider the two point rule for which we first try the polynomial of degree 2. Next, we consider the two point rule for which we first try the polynomial of degree 2.
- Two point rule
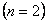
Because of the symmetrical location of the Gauss points, for a two point rule, the Gauss point coordinates must satisfy the relation
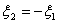 |
(12.11) |
Further, the weights corresponding to these two symmetrically located Gauss points are equal. Thus,
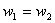 |
(12.12) |
Thus, the two point Gauss quadrature rule becomes:
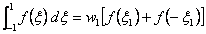 |
(12.13) |
Substituting the polynomial of degree 2 (expression 12.9) into equation (12.13), we get
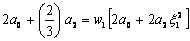 |
(12.14) |
Equating the coefficients of 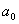 and and 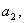 we get we get
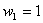 , , |
(12.15a) |
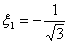 |
(12.15b) |
We choose the negative sign for the square-root in the expression (12.15b), because 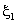 is negative. Using the expressions (12.11),(12.12) and (12.15),the two point Gauss quadrature rule becomes: is negative. Using the expressions (12.11),(12.12) and (12.15),the two point Gauss quadrature rule becomes:
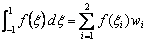 , , |
(12.16a) |
where
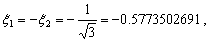 |
(12.16b) |
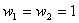 |
(12.16c) |
Note that the sum of the weights is two.
Next, we try the two point rule for the polynomial of degree 3:
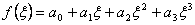 |
(12.17) |
Substituting this expression for 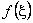 in the two point rule (equation 12.16), we get in the two point rule (equation 12.16), we get
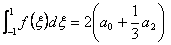 , , |
(12.18) |
that is the exact value. However, when we apply the two point rule to the polynomial of degree 4:
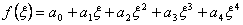 , , |
(12.19) |
we get
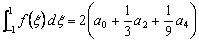 , , |
(12.20) |
that is different than the exact value 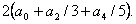 Thus, Thus, 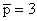 for for 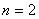 . Next, we consider the three point rule for which we first try the polynomial of degree 4. . Next, we consider the three point rule for which we first try the polynomial of degree 4.
- Three point rule
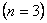
Since the Gauss points are symmetrically located, for a three point rule, the Gauss points must satisfy the relations:
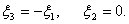 |
(12.21) |
Further, the weights corresponding to the symmetrically located Gauss points must be equal. Thus,
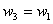 |
(12.22) |
Thus, the three point Gauss quadrature rule becomes:
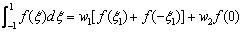 |
(12.23) |
Substituting the polynomial of degree 4 (expression 12.19) into equation (12.23) we get
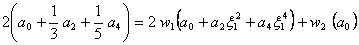 |
(12.24) |
Equating the coefficients of 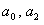 and and 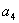 , we get , we get
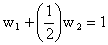 , , |
(12.25a) |
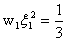 , , |
(12.25b) |
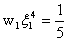 . . |
(12.25c) |
The solution of these three non linear equations is
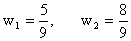 , , |
(12.26a) |
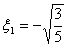 . . |
(12.26b) |
We choose the negative sign for the square-root in the expression (12.26b), because 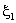 is negative. Using the expressions (12.21),(12.22) and (12.26), the three point Gauss quadrature rule becomes: is negative. Using the expressions (12.21),(12.22) and (12.26), the three point Gauss quadrature rule becomes:
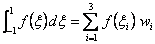 , , |
(12.27a) |
where
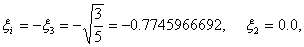 |
(12.27b) |
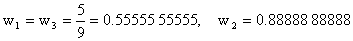 . . |
(12.27c) |
Note that the sum of the weights is two.
It can be easily verified that the three point rule gives the exact value when 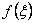 is a polynomial of degree 5 but not 6. is a polynomial of degree 5 but not 6.
In this way, we can find the Gauss point coordinates and the corresponding weight for 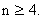 We can also determine the degree of polynomial We can also determine the degree of polynomial 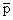 for which this rule gives the exact value. The following table gives the Gauss point coordinates and the corresponding weights upto for which this rule gives the exact value. The following table gives the Gauss point coordinates and the corresponding weights upto 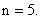 It also indicates the value of It also indicates the value of 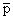 for which the rule is exact. for which the rule is exact.
n |
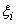
|
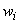
|
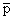
|
1 |
0 |
2 |
1 |
2 |
-0.57735
0.57735 |
1
1 |
3 |
3 |
-0.77460
0
0.77460 |
0.55556
0.88889
0.55556 |
5 |
4 |
-0.86114
-0.33998
0.33998
0.86114 |
0.34786
0.65215
0.65215
0.34786 |
7
|
5 |
-0.90618
-0.53847
0
0.53847
0.90618 |
0.23693
0.47863
0.56889
0.47863
0.23693 |
9 |
Table 12.1
Gauss point coordinates and weights for various values of n. The formula is exact if the function is a polynomial of degree 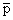 . This data is from the "Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables" by M. Abramowitz and I.A. Stegun, National Bureau of Standards, U.S.A. , 1964 . This data is from the "Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables" by M. Abramowitz and I.A. Stegun, National Bureau of Standards, U.S.A. , 1964
From the above table, we find that the n-point Gauss quadrature rule is exact if the function is a polynomial of degree 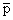 where where 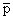 is given by is given by
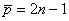 . . |
(12.28) |
Alternately, if we want to integrate a polynomial of degree 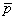 , then, we get the exact value if we use the Gauss quadrature rule where , then, we get the exact value if we use the Gauss quadrature rule where
|