Expressions for Element Stiffness Matrix and Force Vector
The expression for the element stiffness matrix 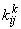 (equation 9.8) is (equation 9.8) is
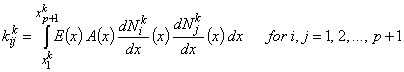 |
(11.46) |
Now, we change the variable of integration from x to 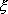 . The integration is from node 1 to node p +1. Therefore, the limits of integration change from . The integration is from node 1 to node p +1. Therefore, the limits of integration change from 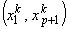 to to 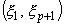 . Since . Since 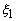 = -1 and = -1 and 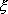 p+1 = +1 (Fig. 11.4), the limits of integration became (-1 ,1 ). Further, when we substitute the expression (11.7) for the mapping function and the expression (11.45) for the shape function derivatives, the integrand becomes p+1 = +1 (Fig. 11.4), the limits of integration became (-1 ,1 ). Further, when we substitute the expression (11.7) for the mapping function and the expression (11.45) for the shape function derivatives, the integrand becomes
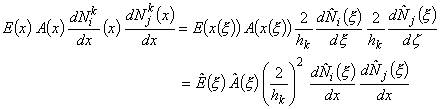 |
(11.47) |
Substituting expression (11.47) for the integrand and expression (11.44) for dx in equation (11.46) and changing the limits of integration as explained above, we get
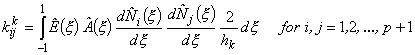 |
(11.48) |
The expression for the element force vector 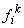 (equation 9.9) is (equation 9.9) is
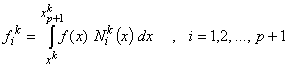 |
(11.49) |
To change the variable of integration from x to 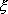 , we proceed in the similar fashion. As explained earlier, the limits of integration change from , we proceed in the similar fashion. As explained earlier, the limits of integration change from 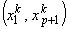 to (-1 ,1 ). Further, when the expressions (11.7) and (11.8) for the mapping function and the shape functions are substituted, the integrand becomes to (-1 ,1 ). Further, when the expressions (11.7) and (11.8) for the mapping function and the shape functions are substituted, the integrand becomes
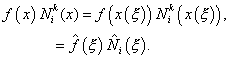 |
(11.50) |
Substituting expression (11.50) for the integrand and expression (11.44) for dx in equation (11.49) and changing the limits of integration to (-1 ,1 ), we get
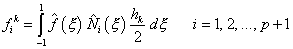 |
(11.51) |
We use expressions (11.48) and (11.51) for evaluating the element stiffness matrix 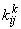 and the element force vector and the element force vector 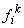 instead of the expressions (11.46) and (11.49). For developing a computer code for the finite element method, the new expressions (11.48) and (11.51) have the following advantages over the older expressions (11.46) and (11.49) instead of the expressions (11.46) and (11.49). For developing a computer code for the finite element method, the new expressions (11.48) and (11.51) have the following advantages over the older expressions (11.46) and (11.49)
- For using the expressions (11.48) and (11.51), the shape functions need to be defined over the master element. Hence, they need to be defined only once.
- Expressions (11.48) and (11.51) are more convenient for using a numerical integration scheme.
A commonly used numerical integration scheme, namely the Gauss-Legendre numerical integration scheme, is discussed in the next lecture.
|