Subroutine SHAPE
This subroutine calculates the values of shape functions Ni and their derivatives 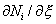 at the given value of natural coordinate at the given value of natural coordinate 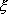 for the given order (p) of approximation. Since for the given order (p) of approximation. Since 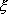 is a natural coordinate its value lies between -1 to 1. Further, we restrict the value of p to only 1, 2 and 3. Note that when the order of approximation is p , the number of nodes per element is p +1. This is also the number of degrees of freedom per element or the number of shape functions. We use the following notation for the variables. is a natural coordinate its value lies between -1 to 1. Further, we restrict the value of p to only 1, 2 and 3. Note that when the order of approximation is p , the number of nodes per element is p +1. This is also the number of degrees of freedom per element or the number of shape functions. We use the following notation for the variables.
deno1, deno2, deno3, deno4 : temporary variables (real)
i : index for do loop (integer)
ndofel : number of degrees of freedom per element (integer)
p : order of the approximation (p)
psi : natural coordinate (real)
dshap (ndofel) : values of the shape function derivatives at given 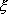
psin (ndofel) : natural coordinates of nodes (real)
shap (ndofel) : shape function values at given x
- OUTPUT Variables : ndofel, shap (ndofel), dshap (ndofel)
Now, the subroutine SHAPE can be written as follows.
Subroutine SHAPE (p, psi, ndofel, shap, dshap)
ndofel = p+1
do i =1, ndofel
psin( i) = -1 + (i-1) * 2/p
enddo
If p = 1, then
shap (1) = (psi - psin(2))/(psin(1) - psin(2))
shap( 2) = (psi - psin(1)) / (psin(2) - psin(1))
dshap (1) = 1 / (psin (1) - p sin(2))
dshap (2) =1/(psin(2) - psin(1))
end if
If p = 2, then
shap (1) = (psi -psin(2)) * (psi - psin(3))/((psin(1)-psin(2)) * (psin(1) - psin(3)))
shap (2) = (psi -psin(3)) * (psi - psin(1))/((psin(2)-psin(3)) * (psin(2) - psin(1)))
shap (3) = (psi -psin(1)) * (psi - psin(2))/((psin(3)-psin(1)) * (psin(3) - psin(2)))
dshap (1) = (psi -psin(3))+(psi - psin(2))/((psin(1)-psin(2)) * (psin(1) - psin(3)))
dshap (2) = (psi -psin(1))+(psi - psin(3))/((psin(2)-psin(3)) * (psin(2) - psin(1)))
dshap (3) = (psi -psin(2))+ (psi - psin(1))/((psin(3)-psin(1)) * (psin(3) - psin(2)))
end if
If p = 3, then
deno 1 = (psin(1) - psin(2)) * (psin(1) - psin(3)) * (psin(1) - psin(4)
deno 2 = (psin(2) - psin(3)) * (psin(2) - psin(4)) * (psin(2) - psin(1)
deno 3 = (psin(3) - psin(4)) * (psin(3) - psin(1)) * (psin(3) - psin(2)
deno 4 = (psin(4) - psin(1)) * (psin(4) - psin(2)) * (psin(4) - psin(3)
shap (1) = (psi -psin(2)) * (psi - psin(3))*(psi-psin(4)) /deno 1
shap (2) = (psi -psin(3)) * (psi - psin(4))*(psi-psin(1)) /deno 2
shap (3) = (psi -psin(4)) * (psi - psin(1))*(psi-psin(2)) /deno 3
shap (4) = (psi -psin(1)) * (psi - psin(2))*(psi-psin(3)) /deno 4
dshap (1) = ((psi -psin(3))*(psi - psin(4))+(psi-psin(2))*(psi-psin(4))
+(psi-psin(2))*(psi-psin(3)))/deno 1
dshap (2) = ((psi -psin(4))*(psi - psin(1))+(psi-psin(3))*(psi-psin(1))
+(psi-psin(3))*(psi-psin(4)))/deno 2
dshap (3) = ((psi -psin(1))*(psi - psin(2))+(psi-psin(4))*(psi-psin(2))
+(psi-psin(4))*(psi-psin(1)))/deno 3
dshap (4) = ((psi -psin(2))*(psi - psin(3))+(psi-psin(1))*(psi-psin(3))
+(psi-psin(1))*(psi-psin(2)))/deno 4
end if Note that the following things should be kept in mind while writing the computer codes :
- Meaningful symbols should be used to denote the variables. For example ndofel for denoting the number of degrees of freedom per element
- A group of statements should be indented to identify various steps and sub steps.
- A generous amount of comment statements should be inserted to provide explanation for the following group of statements.
|