| |
In order to analyse such continuous systems one has to take recourse of either Rayleigh Ritz (RR) approach or Finite Element Analysis (FEA). Even though FEA is used more frequently, in this lecture the RR approach ([13-4]) is followed since it yields closed form results. Such models are useful for characterization of ACLD systems and simulation of their performance. The RR approach follows representation of displacements in terms of assumed shape functions. For studying the effect of flexural motion, two significant displacements, assumed in series form are longitudinal displacement of the centre of the viscoelastic layer 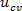 , and the transverse displacement of the host-beam , and the transverse displacement of the host-beam 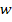 . Accordingly, the following relations are useful for deriving the governing equation of motion: . Accordingly, the following relations are useful for deriving the governing equation of motion:
where, b and c are vectors of unknown time varying coefficients which satisfy the initial conditions related to the vibration. Ignoring the mass of viscoelastic and piezoelectric layer, passive loss-factors for the host beam, constraining and the piezo-layers, and assuming that the host beam is completely covered by the damping layers; one can obtain the simplified governing equation of motion as:
In Eqn. (39.2), m – refers to the mass per unit length, A - cross-sectional area, t – thickness, l– beam length,
η – loss factor, I – area moment of inertia, V is 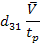 (d31 – piezoelectric constant and
V the applied voltage; subscripts b, v and p denote the base beam, viscoelastic and piezoelectric material respectively. (d31 – piezoelectric constant and
V the applied voltage; subscripts b, v and p denote the base beam, viscoelastic and piezoelectric material respectively. |