Here,
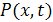 is the generalized distributed load on the beam and P0 and M0 are concentrated load and moment on the beam applied at x = x0. is the generalized distributed load on the beam and P0 and M0 are concentrated load and moment on the beam applied at x = x0.
The higher order terms in mass viz.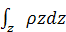 and and 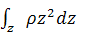 are neglected. It is to be noted that for distributed control, there is an interesting difference in forming the equation of motion of the system. In the usual expression of Hamiltonian, the actuation of the structure is considered as an outside effect and the work done due to actuation is considered separately, whereas in this approach, the effect of actuator is considered implicitly in the evaluation of elastic strain (eqns. (28.3) and (28.5). It is assumed that the total strain in the beam is governed by the displacement assumption corresponding to the beam model and the actual elastic strain is the difference between the total strain and the active strain. are neglected. It is to be noted that for distributed control, there is an interesting difference in forming the equation of motion of the system. In the usual expression of Hamiltonian, the actuation of the structure is considered as an outside effect and the work done due to actuation is considered separately, whereas in this approach, the effect of actuator is considered implicitly in the evaluation of elastic strain (eqns. (28.3) and (28.5). It is assumed that the total strain in the beam is governed by the displacement assumption corresponding to the beam model and the actual elastic strain is the difference between the total strain and the active strain.
The advantage of this approach is that the control force comes out as an integral part of the model unlike a forcing function in the conventional approach.
In the next lecture, we will exemplify the controller design corresponding to this system.
Congratulations! You have finished Lecture 28. |