Modelling of Active Distributed Vibration Control System:
In this section, for developing distributed vibration control system, proportional velocity feedback closed loop control algorithm is employed as a control law. It is also assumed, that the sensing is distributed and continuous in space and time. For simplicity, the host beam is considered to be slender, so that the effect of rotary inertia and shear deformation can be neglected. The single layer theory of composite beam is used for modelling of the host beam. The flexural motion of the beam in xoz plane can be modeled by taking the displacement field as
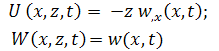 |
(28.1) |
(,x) denotes differentiation with respect to x. The total strain in any (i-th) layer of the beam consists of two parts; the elastic strain  given by given by
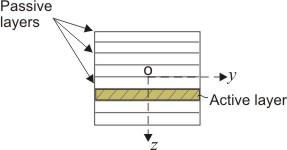
Figure 28.1: Composite laminate with smart layers
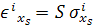 |
(28.2) |
and the active strain 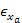 , present only in the active layer. Thus, the expression for strain in any layer can generally be written as , present only in the active layer. Thus, the expression for strain in any layer can generally be written as
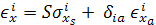 |
(28.3) |
Here, δia is the Kronecker's delta and its value is 1 when i = a, (i.e. for active layer) and is zero for other layers. Also, from the constitutive relationship; for isotropic active layer, the compliance modulus 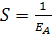 and for orthotropic composite layers with fibre-angle θ, the same may be expressed as: and for orthotropic composite layers with fibre-angle θ, the same may be expressed as:
where 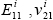 etc. are Elastic constants and Poisson’s ratio respectively; etc. are Elastic constants and Poisson’s ratio respectively; 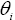 is the ply-angle at this i-th layer. is the ply-angle at this i-th layer.
Following Euler - Bernoulli model, the total strain at any layer may also be expressed as
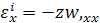 |
(28.5) |
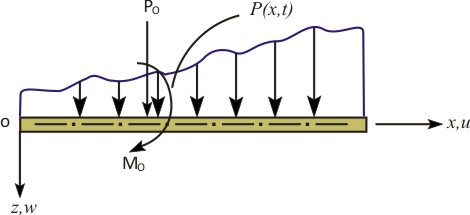
Figure 28.2: A composite beam under generalized loading
|