In the steady state, the solutions of the governing equations are assumed to be
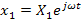 and and
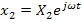 . Substituting these in eqns (16.1) and (16.2),
we get . Substituting these in eqns (16.1) and (16.2),
we get
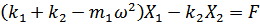 |
(16.3) |
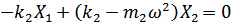 |
(16.4) |
Solving eqns. (16.3) and (16.4), we obtain
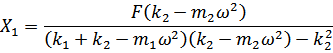 |
(16.5) |
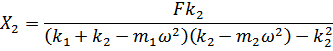 |
(16.6) |
From eqns. (16.5) and (16.6), you may note that if the secondary system is tuned to the excitation frequency, i.e., its natural frequency 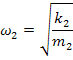 is made equal to is made equal to 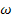 , then , then 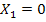 and and 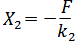 . This implies that the primary system comes to rest, after tuning. . This implies that the primary system comes to rest, after tuning.
|