Model of a Simple Vibration Neutralizer
The primary system is assumed to be an undamped single-degree-of-freedom system of mass 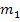 and
stiffness and
stiffness 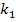 . The secondary system (the neutralizer) consists
of mass . The secondary system (the neutralizer) consists
of mass 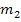 attached to the primary using a spring of stiffness attached to the primary using a spring of stiffness 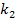 . The primary system is subjected to a harmonic excitation . The primary system is subjected to a harmonic excitation 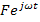 as shown in figure 16.1. as shown in figure 16.1.
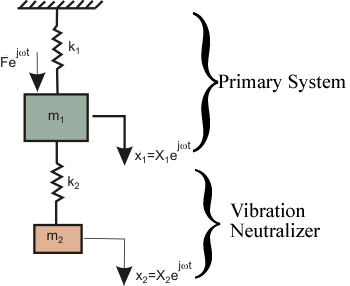
Figure 16.1: Vibration neutralizer
The responses of the masses from
their respective equilibrium positions are denoted as 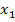 for for 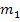 and and 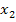 for for 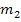 . The equations of motion for the masses can be written as . The equations of motion for the masses can be written as
| |
(16.1) |
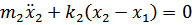 |
(16.2) |
|