Error Propagation
Associated with each measured variable 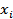 is an uncertainty is an uncertainty
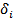 originating from scatter. Uncertainty in universal constants such as acceleration due to gravity and fluid properties can be treated as negligible in comparison to originating from scatter. Uncertainty in universal constants such as acceleration due to gravity and fluid properties can be treated as negligible in comparison to
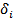 .
It is quite common to construct a new quantity .
It is quite common to construct a new quantity
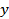 from the measured quantities from the measured quantities
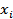 .
For example, a combination of pitot static tube and manometer measures a pressure difference ( .
For example, a combination of pitot static tube and manometer measures a pressure difference (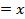 ) and velocity ( ) and velocity (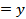 )
is recovered through a square root formula. It is of interest to determine the uncertainty )
is recovered through a square root formula. It is of interest to determine the uncertainty
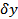 in terms of those in in terms of those in 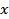 , namely , namely 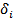 . Since . Since
the following mathematical identity holds:
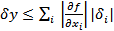
In most applications, 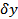 thus determined is substantially larger than the true uncertainty. A closer unbiased estimate used in engineering is thus determined is substantially larger than the true uncertainty. A closer unbiased estimate used in engineering is
In many instances, the partial derivative of function 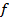 with with 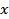 is of order unity; in any case it serves effectively as a scale factor. Hence, is of order unity; in any case it serves effectively as a scale factor. Hence, 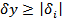 for each for each 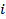 , and Equation 1 is called the error propagation formula. , and Equation 1 is called the error propagation formula.
|