Quantitative analysis and validation
The Rayleigh-Bernard (R-B) experiment is conducted to demonstrate and quantitatively validate the data
analysis procedure of the color schlieren technique. Figure 3 shows the transient sequence of color
schlieren images of R-B convection. Initially, the beam is focused at the red region of the color filter,
Figure 3(a), which is used as the reference image for subsequent calculations. After recording the base
image, a temperature difference is applied between the top and bottom walls of the cavity by circulating
cold and hot water in the respective tanks. Unstable density gradients are created in the fluid medium as
the air near the top cold wall becomes denser compared to air near the lower hot wall, setting up
convection currents across the cavity. The density gradients lead to a change in the index of refraction of the
media and the light beam deflects from its original path. The deflected beam falls on various regions of
the color filter depending on the strength of the refractive index gradient, creating a range of colors.
Figure 3(f) shows the steady state convection pattern. Here, a large color variation is observed near the
horizontal walls and no color variation is seen in the central region. This is due to high thermal gradients
in the near wall region because of diffusion mode of heat transfer compared to the central region, where
convection mode is predominant. The color change near the vertical sides is not very prominent because
of the insulated boundary conditions. Thus, the color schlieren image clearly brings out the thermal
boundary-layer type of the flow structure in the cavity with an overall circulation loop.
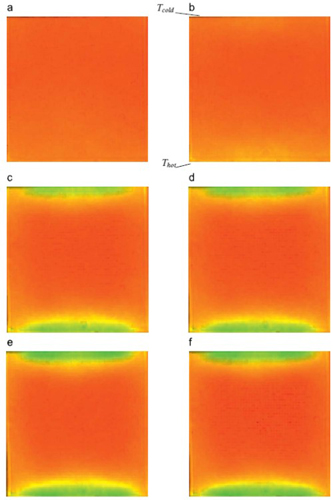
Figure 3: Transient evolution of the convective ield in an ir filled rectangular cavity with top surface temperature, 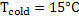 and bottom surface temperature and bottom surface temperature 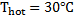 The corresponding Rayleigh number is Ra=48,000: (a) base image (t=0 h); (b) t=0.25 h; (c) t=0.5h; (d) t=1; (e) t=2h and (f) t=4h The corresponding Rayleigh number is Ra=48,000: (a) base image (t=0 h); (b) t=0.25 h; (c) t=0.5h; (d) t=1; (e) t=2h and (f) t=4h
|