Results obtained with complete projection data (marked 100% in 5.18b(i)) and partial data (60% in 5.18b(ii) and 30% in 5.18b(iii), symmetrically placed about the center) are also shown. The axisymmetric nature of temperature distribution is brought out in all the reconstructions. This can be taken as a validation of the extrapolation procedure used to convert partial to an approximate but complete data set. A quantitative comparison of the reconstructed temperature profiles along the diameter of the cavity for different combinations of rays and views are shown in Figure 5.18(c). Profiles obtained with full as well as partial data are reported. For the complete data set, a perfect match between the original and reconstructed profiles can be seen for grid sizes of 128 X 128 and 256 X 256, while small errors are to be seen for the 64 X 64 grid. The extent of deviation from the original increases as the fraction of incomplete data increases. Noticeable errors are to be seen when only 30% of the original data is used, the rest of it being derived by extrapolation. Errors in reconstruction were found to be significantly higher when the partial data set was used without extrapolation.
The magnitudes of errors as a function of discretization of the fluid layer and size of the partial data set are summarized in Table 1. Since the difference between the minimum and maximum temperatures is unity, the percentage error is obtained as 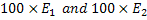 . .
Table 1: Comparision of the original and reconstructed temperature feilds in terms of errors 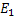 and and 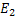 for buoyancy-driven convection in a circular cavity. for buoyancy-driven convection in a circular cavity.
Data Type |
Rays X Views |
|
|
Full Data |
256 X 256 |
0.052 |
0.028 |
128 X 128 |
0.109 |
0.056 |
64 X 64 |
0.124 |
0.058 |
Partial Data |
60% |
256 X 256 |
0.095 |
0.039 |
128 X 128 |
0.148 |
0.061 |
64 X 64 |
0.152 |
0.067 |
30% |
256 X 256 |
0.122 |
0.051 |
128 X 128 |
0.148 |
0.072 |
64 X 64 |
0.173 |
0.076 |
. In Table 1, error 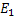 is consistently seen to be higher than is consistently seen to be higher than 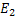 the latter being an average over the entire field. Both errors decrease as the grid size (number of rays and views) increases. For a given grid size, errors increase as the fraction of original data used in reconstruction decreases. When only 30% of the original is used (the rest being obtained by extrapolation), the maximum errors on a 64 X 64 grid are 17.3% (absolute maximum) and 7.6% (RMS). Figure 5.18 shows that the corresponding reconstructions are qualitatively meaningful, and hence these error magnitudes may be taken to be within limits. the latter being an average over the entire field. Both errors decrease as the grid size (number of rays and views) increases. For a given grid size, errors increase as the fraction of original data used in reconstruction decreases. When only 30% of the original is used (the rest being obtained by extrapolation), the maximum errors on a 64 X 64 grid are 17.3% (absolute maximum) and 7.6% (RMS). Figure 5.18 shows that the corresponding reconstructions are qualitatively meaningful, and hence these error magnitudes may be taken to be within limits.
|