Under steady conditions, the average wall heat flux is also equal to the energy transferred across any horizontal plane of the cavity.  Average heat transfer rates at the hot and the cold walls of the cavity have been calculated in terms of Nusselt number and presented in Table 2. Further, they have been compared against an experimental correlation. The correlation summarizes the observations of a number of authors and cavity dimensions. Consequently, it has a large uncertainty level of +20%. The average Nusselt numbers predicted by the two optical techniques match well with each other, with a maximum difference of +5%, that occurs at the lowest Rayleigh number (Ra= 1.3×10⁴) of the present work. The hot and cold wall Nusselt numbers are also reasonably close, indicating a good energy balance in the data reduction procedure. The discrepancies are higher in interferometry at this Rayleigh number owing to the formation of just a few fringes in the cavity.

Table 2: Wall-averaged Nusselt numbers at the lower (hot) and the upper (cold) walls for convection in a rectangular cavity with air as the working fluid. Comparision of experiments with corelation of Gebhart et al (1988). Symbol I in brackets indicates values calculated from interferograms; symbols S indicates values calculated from a schlieren image.

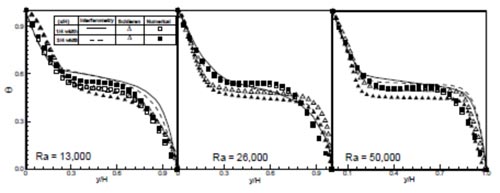
Figure 5.21: Convection in an air-filled cavity. Non-Dimensional temperature profiles as a function of the vertical coordiante.