Shadowgraph
The shadowgraph arrangement depends on the change in the light intensity arising from beam displacement from its original path. Shadowgraph analysis requires tracing the path of individual rays through the aqueous solution. When subjected to linear approximations that include small displacement of the light ray, a second order partial differential equation can be derived for the refractive index field with respect to the intensity contrast in the shadowgraph image. With 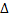 as the distance of the screen from the optical window on the beaker and as the distance of the screen from the optical window on the beaker and 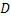 as the Laplace operator in the as the Laplace operator in the 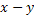 plane, this equation is plane, this equation is
Equations 2 and 5 have to be suitably integrated to determine the refractive index, and hence the concentration field. Integration of the Poisson equation (5) can be performed by a numerical technique, say the method of finite differences. When the approximations involved in Equations 2 and 5 do not apply, optical techniques can be used for flow visualization alone.
In interferometry, one can measure concentration values only at those points where fringes appear. The quantity of information is also limited by the number of fringes (infinite fringe setting) or their deformation (wedge fringe setting). Schlieren and shadowgraph generate information about the refractive index field at every pixel of the image in the form of intensities.
|