Contd...
where 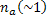 is the refractive index of the ambient, is the refractive index of the ambient, 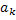 is the size of the focal spot at the knife edge, and is the size of the focal spot at the knife edge, and 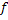 is the focal length of the de-collimating mirror. This equation shows that the schlieren technique records the average gradient of refractive index over the path of the light beam. In terms of the ray-averaged refractive index, the governing equation for the schlieren process can be derived as: is the focal length of the de-collimating mirror. This equation shows that the schlieren technique records the average gradient of refractive index over the path of the light beam. In terms of the ray-averaged refractive index, the governing equation for the schlieren process can be derived as:
where 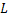 is the length of the path traversed by the light beam through the growth chamber, namely its diameter. Equation 3 requires the approximation that changes in the light intensity occur due to beam deflection, rather than its physical displacement. The concentration gradient is related with the refractive-index gradient of the KDP solution using the following relation is the length of the path traversed by the light beam through the growth chamber, namely its diameter. Equation 3 requires the approximation that changes in the light intensity occur due to beam deflection, rather than its physical displacement. The concentration gradient is related with the refractive-index gradient of the KDP solution using the following relation
Here 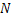 is the molar concentration of the solution and a is the polarizability of the KDP crystal is the molar concentration of the solution and a is the polarizability of the KDP crystal 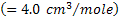 Combining Equations 3 and 4 and integrating from a location in the bulk of the solution (where the gradients are negligible), the concentration distribution around the growing crystal can be uniquely determined. Combining Equations 3 and 4 and integrating from a location in the bulk of the solution (where the gradients are negligible), the concentration distribution around the growing crystal can be uniquely determined.
The contribution of refraction of light at the confining optical windows has been accounted for by applying a correction factor in Equation 3 for the angle of deflection with which the beam emerges from the growth chamber. It can be shown using Snell’s law that the correction factor is equal to the refractive index of the KDP solution (=1.355) at the ambient temperature. |