A quantitative assessment of the reconstructed temperature field is taken up next. To compute errors, a reference solution is required. Since this is not available for experimental data, the following strategy has been adopted. The temperature field obtained by merging the S-shaped curves in the two projections has been taken as the reference solution. The temperature field thus developed satisfies exactly the energy balance criterion. Errors have been determined between the temperature field developed frsom the thinning algorithms and the reference solution. Errors reported are the absolute maximum error 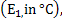 the RMS error the RMS error 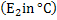 and the percentage RMS error and the percentage RMS error 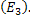 The percentage RMS error has been calculated with respect to the temperature different across the fluid layer. The completed fluid layer has been considered while obtaining these quantities. The errors for each thinning algorithm have been summarized in Table 2. The percentage RMS error has been calculated with respect to the temperature different across the fluid layer. The completed fluid layer has been considered while obtaining these quantities. The errors for each thinning algorithm have been summarized in Table 2.
An examination of Table 2 shows that errors associated with the automatic thinning algorithm are uniformly small. The absolute maximum errors with the other algorithms are larger, being in excess of 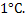 This may not be acceptable in many applications. A comparison of the absolute maximum and RMS errors shows the latter to be smaller, by more than a factor of two. This suggests that large errors are localized over the flow field. The percentage RMS error is truly small for the automatic thinning algorithm, while it is in the range This may not be acceptable in many applications. A comparison of the absolute maximum and RMS errors shows the latter to be smaller, by more than a factor of two. This suggests that large errors are localized over the flow field. The percentage RMS error is truly small for the automatic thinning algorithm, while it is in the range 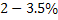 for the curve fitting and paintbrush methods. This range may still be acceptable in engineering measurement. for the curve fitting and paintbrush methods. This range may still be acceptable in engineering measurement.
Table 2: Reconstruction Errors from the Fringe Thinning Algorithms
Errors |
Automatic Fringe Thinning |
Curve Fitting Method |
Paintbrush Method |
|
0.034 |
1.51 |
1.03 |
|
0.011 |
0.60 |
0.34 |
|
0.066 |
3.51 |
2.01 |
|