| |
Since intensity varies as 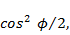 , the corresponding phase difference
for a fringe shift is , the corresponding phase difference
for a fringe shift is 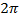 . The equivalent optical path difference is . The equivalent optical path difference is 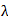 . The interference fringes
are ordered i.e. the . The interference fringes
are ordered i.e. the 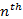 fringe counted for example from the left will represent a phase
difference of fringe counted for example from the left will represent a phase
difference of 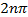 with respect to the reference wave. In distance measurements an integer
number of fringe shifts is used and hence the resolution in distance measurement is with respect to the reference wave. In distance measurements an integer
number of fringe shifts is used and hence the resolution in distance measurement is 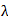 . .
In a given problem, individual portions of the light beam traverse distinct optical
paths and the phase difference is a spatially distributed variable. In an interferometric
measurement, this beam combined with one that has a constant phase. In regions where
the phase difference between the two is 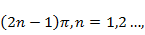 the intensity of the combined
beam is zero and we get destructive interference. When the phase difference is the intensity of the combined
beam is zero and we get destructive interference. When the phase difference is 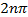 we
get constructive interference. The corresponding path differences are we
get constructive interference. The corresponding path differences are 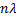 and and 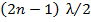 respectively. The phase field in the form of a fringe pattern can be recorded, say by a
camera, to extract information about the primary variables of the problem being studied.
In applications, quantitative measurements are possible if lines of constant phase exist so
that fringes form, and a fringe shift can be identified from one fringe to another. respectively. The phase field in the form of a fringe pattern can be recorded, say by a
camera, to extract information about the primary variables of the problem being studied.
In applications, quantitative measurements are possible if lines of constant phase exist so
that fringes form, and a fringe shift can be identified from one fringe to another.
|